如图，A，B是海面上位于东西方向相距海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距海里的C点的救援船立即即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？

【解析】本试题考查了利用正弦定理和余弦定理求解三角形的实际运用。并考查了分析问题和解决问题的能力。

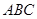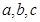在△中，分别为内角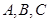的对边，且．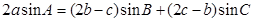

(1)求角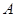的大小；

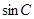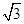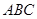(2)若＋＝，试判断△的形状．

【解析】本试题主要考查了解三角形中正弦定理和余弦定理的运用。求解变和角，并定形的问题。

在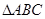中，角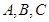的对边分别为，。

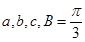（1）求的值；

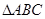（2）求的面积.

【解析】本试题主要是考查了解三角形中正弦定理和三角形面积公式的运用。

已知在△ABC中，角A、B、C所对的边分别为a，b，c，且。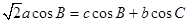

（1）求角B的大小；

（2）设向量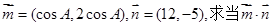取最大值时，tanC的值。

【解析】本试题主要是考查了解三角形中正弦定理的运用，先求解B，然后，利用数量积公式我们表示向量积，从而借助于三角形中值域来求解C的正切值。

已知中，内角的对边的边长分别为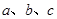，且

（I）求角的大小；

（II）若求的最小值．

【解析】第一问，由正弦定理可得：sinBcosC=2sinAcosB-sinCcosB，即sin(B+C)=2sinAcosB，

第二问，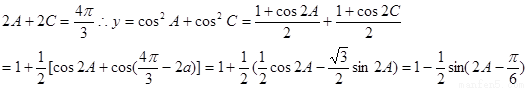

三角函数的性质运用。

解：（Ⅰ）由正弦定理可得：sinBcosC=2sinAcosB-sinCcosB，即sin(B+C)=2sinAcosB， 

（Ⅱ）由（Ⅰ）可知 

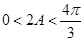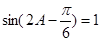,，则当 ,即时，y的最小值为．