
题目列表(包括答案和解析)
在△ABC中,b=2,B=45°,如果利用正弦定理解此三角形时,有两解,求a的取值范围.
在△ABC中,已知b=2,B=45°,如果用正弦定理解三角形有两解,则边长a的取值范围是
2<a<2![]()
2<a<4
![]() <a<2
<a<2
![]() <a<2
<a<2![]()
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.[来源:学,科,网Z,X,X,K]
【解析】第一问解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
(11)由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
【解析】如图:|OB|=b,|O F1|=c.∴kPQ=![]() ,kMN=﹣
,kMN=﹣![]() .
.
直线PQ为:y=![]() (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=![]() x.由
x.由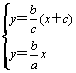 ,得:Q(
,得:Q(![]() ,
,![]() );由
);由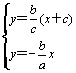 ,得:P(
,得:P(![]() ,
,![]() ).∴直线MN为:y-
).∴直线MN为:y-![]() =﹣
=﹣![]() (x-
(x-![]() ),
),
令y=0得:xM=![]() .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=![]() ,解之得:
,解之得:![]() ,即e=
,即e=![]() .
.
【答案】B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com