（本小题满分12分）
为了研究某高校大学新生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图如下图所示，已知后6组的频数从左到右依次是等差数列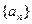的前六项。
（1）试确定视力介于4.9至5.0的抽查学生的人数。
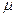（2）若规定视力低于5.0的学生属于近视学生，试估计该校新生的近视率的大
小。

（本小题满分12分）

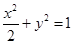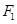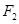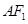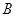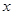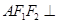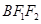已知椭圆的左、右焦点为、，上顶点为A，直线交椭圆于. 如图所示沿轴折起，使得平面平面. 点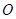为坐标原点.

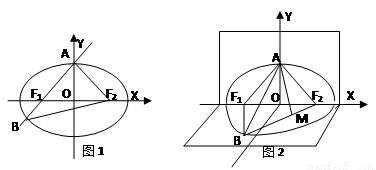
( I ) 求三棱锥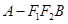的体积；

（Ⅱ）线段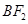上是否存在点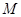，使得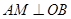，若存在，请在图1中指出点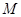的坐标；若不存在，请说明理由.

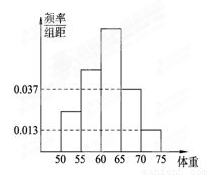
（本小题满分12分）为了解今年某校高三毕业班准备报考飞行员学生的体重情

况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前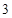个小组的频率之比为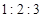，其中第小组的频数为.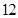

(1)求该校报考飞行员的总人数;

(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望.

（本小题满分12分）在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形的高的比为2:3:4:6:4:1，第三组的频数为12，请解答下列问题：

    （1）本次活动共有多少件作品参加评比？

    （2）哪组上交的作品数量多？有多少件？

    （3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率较高？

（本小题满分12分）

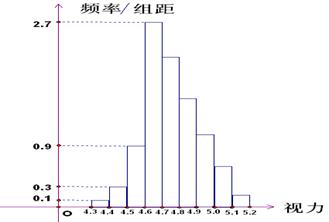
为了研究某高校大学新生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图如下图所示，已知后6组的频数从左到右依次是等差数列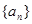的前六项。

（1）试确定视力介于4.9至5.0的抽查学生的人数。

（2）若规定视力低于5.0的学生属于近视学生，试估计该校新生的近视率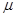的大

小。