
题目列表(包括答案和解析)
椭圆![]() 的一条弦PQ过它的右焦点且垂直于x轴,以线段PQ为直径作圆C,则点A(a,0)与圆C的位置关系是
的一条弦PQ过它的右焦点且垂直于x轴,以线段PQ为直径作圆C,则点A(a,0)与圆C的位置关系是
[ ]
A.点A在圆C内 B.点A在圆C上
C.点A在圆C外 D.以上三种情况都可能
(1)求椭圆C的方程;
(2)已知A为椭圆C的左顶点,直线l过右焦点F2与椭圆C交于M、N两点,若AM、AN的斜率k1,k2满足k1+k2=![]() ,求直线l的方程;
,求直线l的方程;
(3)已知P是椭圆C上位于第一象限内的点,△PF1F2的重心为G,内心为I,求证:IG∥F1F2.
| x2 |
| m |
| y2 |
| n |
| QF |
| FP |
| x2 |
| m |
| y2 |
| n |
| x2 |
| m |
| y2 |
| n |
| x2 |
| m |
| y2 |
| n |
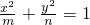 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.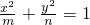 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com