
题目列表(包括答案和解析)
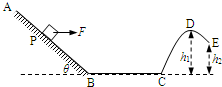
如图,AB为粗糙的长直斜面,动摩擦因数μ=0.4,与水平方向的夹角θ=37°,BC为光滑水平面,CDE为光滑曲面,B、C两接口处均光滑连接。D、E两点离水平地面的高度分别为h1=8.64m,h2=4m。一质量m=0.20kg的滑块由斜面上某一点P从静止开始下滑,在斜面上始终受一水平向右恒力F=1N的作用,到达B点时立即撤去拉力F,从P点到达C点共经历t=3s。已知PB与BC长度之和为32m。求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
(1)滑块沿AB段运动时加速度a和所用时间t1;
(2)若水平向右恒力F大小可调,则恒力F在何范围内可使滑块沿PB、BC运动越过曲面落地。某同学对第二问的解答如下:若要使滑块越过曲面落地,则离开曲面E点时的速度至少为0。从P点至E点列出动能定理。即可求得所需的最小恒力。请判断该同学的解答是否正确,并说明理由,若该同学解答错误则求出正确的恒力范围。

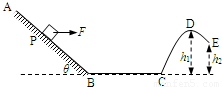
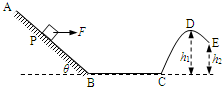 (2013?徐汇区二模)如图,AB为粗糙的长直斜面,动摩擦因数μ=0.4,与水平方向的夹角θ=37°,BC为光滑水平面,CDE为光滑曲面,B、C两接口处均光滑连接.D、E两点离水平地面的高度分别为h1=8.64m,h2=4m.一质量m=0.20kg的滑块由斜面上某一点P从静止开始下滑,在斜面上始终受一水平向右恒力F=1N的作用,到达B点时立即撤去拉力F,从P点到达C点共经历t=3s.已知PB与BC长度之和为32m.求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
(2013?徐汇区二模)如图,AB为粗糙的长直斜面,动摩擦因数μ=0.4,与水平方向的夹角θ=37°,BC为光滑水平面,CDE为光滑曲面,B、C两接口处均光滑连接.D、E两点离水平地面的高度分别为h1=8.64m,h2=4m.一质量m=0.20kg的滑块由斜面上某一点P从静止开始下滑,在斜面上始终受一水平向右恒力F=1N的作用,到达B点时立即撤去拉力F,从P点到达C点共经历t=3s.已知PB与BC长度之和为32m.求:(sin37°=0.6,cos37°=0.8,g=10m/s2)粗糙水平地面上有一质量为30 Kg的滑块,在斜向上的拉力F的作用下向右滑动.已知滑块与地面间的动摩擦因数为1/3,拉力F与水平面间夹角为37°,大小为160 N.求滑块的加速度.(g取10 m/s2,sin37°=0.6,cos37°=0.8)
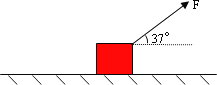
要求:能作出正确的受力分析图,并能将力正确分解,没有受力分析图的只得一半分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com