
题目列表(包括答案和解析)
| q | m |
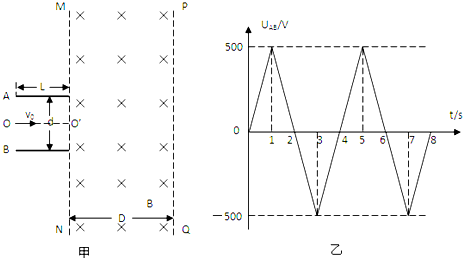
| q | m |
| ||
| 10 |
| ||
| 2 |
| q |
| m |
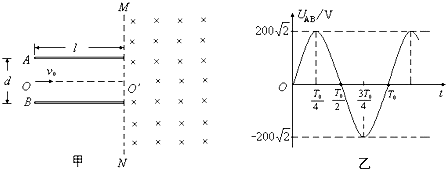
如图甲所示,两平行金属板A、B的板长L=0.2m,板间距d=0.2m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应。在金属板右侧有一方向垂直于纸面向里的匀强磁场,其左右宽度D=0.4m,上下范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B=1×10-2 T.现从t=0开始,从两极板左侧的中点O处以每秒钟1000个的数量均匀连续地释放出某种正电荷粒子,这些粒子均以v0=2×105 m/s的速度沿两板间的中线OO′连续进入电场,已知带电粒子的比荷=1×108C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求: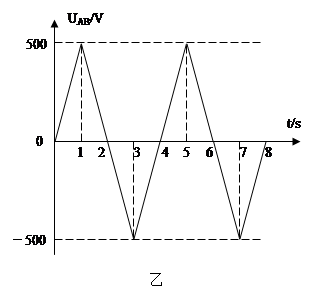
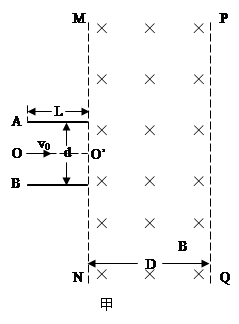
(1)t=0时刻进入的粒子,经边界MN射入磁场和射出磁场时两点间的距离;
(2)在0~1s内有多少个带电粒子能进入磁场;
(3)何时由O点进入的带电粒子在磁场中运动的时间最长?
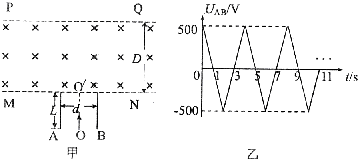
如图甲所示,两平行金属板A、B的板长L=0.2m,板间距d=0.2m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应,在金属板上侧有一方向垂直于纸面向里的匀强磁场,其上下宽度D= 0.4m,左右范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B =1×l0-2T.在极板下侧中点O处有一粒子源,从t=0时起不断地沿着OO’发射比荷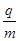 =1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.
=1×l08 C/kg.初速度为v0=2×l05m/s的带正电粒子,忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化.
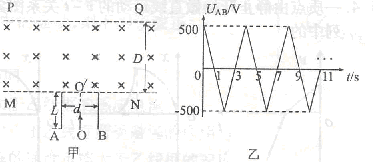
(1)求粒子进入磁场时的最大速率;
(2)对于能从MN边界飞出磁场的粒子,其在磁场的入射点和出射点的间距s是否为定值?若是,求该值;若不是,求s与粒子由O出发的时刻t之间的关系式;
(3)定义在磁场中飞行时间最长的粒子为{A类粒子},求出{A类粒子}在磁场中飞行的时间,以及由O出发的可能时刻.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com