一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量Δω与对应时间Δt的比值定义为角加速度β（即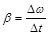）．我们用电磁打点计时器、刻度尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50 Hz，A、B、C、D……为计数点，相邻两计数点间有四个点未画出）

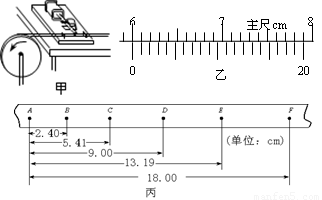
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；

②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；

③经过一段时间，停止转动和打点，取下纸带，进行测量．

（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为        cm；

（2）由图丙可知，打下计数点D时，圆盘转动的角速度为          rad/s；（取二位有效数字，下同）

（3）纸带运动的加速度大小为         m/s²，圆盘转动的角加速度大小为            rad/s²；

（4）如果实验测出的角加速度值偏大，其原因可能是                             （写出1条）．

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△与对应时间△t的比值定义为角加速度β（即）．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D……为计数点，相邻两计数点间有四个点未画出）

①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；

②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；

③经过一段时间，停止转动和打点，取下纸带，进行测量．

   （1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为      cm；

   （2）由图丙可知，打下计数点D时，圆盘转动的角速度为_      rad/s；

   （3）纸带运动的加速度大小为       m/s2，圆盘转动的角加速度大小为      rad/s2；

   （4）如果实验测出的角加速度值偏大，其原因可能是         （至少写出1条）．

II．（9分）2010年诺贝尔物理学奖授予英国曼彻斯特大学科学家安德烈·海姆和康斯坦丁·诺沃肖洛夫，以表彰他们对石墨烯的研究，他们最初是用透明胶带从石墨晶体上“粘”出一片石墨烯的．我们平常所用的铅笔芯中就含有石墨，能导电．某同学设计了探究铅笔芯伏安特性曲线的实验，得到如下数据（I和U分别表示通过铅笔芯的电流和其两端的电压）：实验室提供如下器材：

    A．电流表A1（量程0.6A，内阻约为1.0Ω）

    B．电流表A2（量程3A，内阻约为0.1Ω）

    C．电压表V1（量程3V，内阻3kΩ）

    D．电压表V2（量程15V，内阻15kΩ）

    E．滑动变阻器R1（阻值0～10Ω，额定电流2A）

    F．滑动变阻器R2（阻值0～2kΩ，额定电流0.5A）

   （1）除长约14cm的中华绘图2B铅笔芯、稳压直流电源E（6V）、开关和带夹子的导线若干外，还需选用的其它器材有         （填选项前字母）（2）在虚线方框中画出实验电路图；

   （3）根据表格中数据在坐标纸上画出铅笔芯的I-U图线．

；

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量Δω与对应时间Δt的比值定义为角加速度β（即）．我们用电磁打点计时器、刻度尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50 Hz，A、B、C、D……为计数点，相邻两计数点间有四个点未画出）

①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，停止转动和打点，取下纸带，进行测量．
（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为       cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为         rad/s；（取二位有效数字，下同）
（3）纸带运动的加速度大小为        m/s²，圆盘转动的角加速度大小为           rad/s²；
（4）如果实验测出的角加速度值偏大，其原因可能是                            （写出1条）．

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△与对应时间△t的比值定义为角加速度β（即）．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D……为计数点，相邻两计数点间有四个点未画出）

①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；

②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；

③经过一段时间，停止转动和打点，取下纸带，进行测量．

   （1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为      cm；

   （2）由图丙可知，打下计数点D时，圆盘转动的角速度为_      rad/s；

   （3）纸带运动的加速度大小为      m/s2，圆盘转动的角加速度大小为      rad/s2；

   （4）如果实验测出的角加速度值偏大，其原因可能是        （至少写出1条）．

II．（9分）2010年诺贝尔物理学奖授予英国曼彻斯特大学科学家安德烈·海姆和康斯坦丁·诺沃肖洛夫，以表彰他们对石墨烯的研究，他们最初是用透明胶带从石墨晶体上“粘”出一片石墨烯的．我们平常所用的铅笔芯中就含有石墨，能导电．某同学设计了探究铅笔芯伏安特性曲线的实验，得到如下数据（I和U分别表示通过铅笔芯的电流和其两端的电压）：实验室提供如下器材：

    A．电流表A1（量程0.6A，内阻约为1.0Ω）

    B．电流表A2（量程3A，内阻约为0.1Ω）

    C．电压表V1（量程3V，内阻3kΩ）

    D．电压表V2（量程15V，内阻15kΩ）

    E．滑动变阻器R1（阻值0～10Ω，额定电流2A）

    F．滑动变阻器R2（阻值0～2kΩ，额定电流0.5A）

   （1）除长约14cm的中华绘图2B铅笔芯、稳压直流电源E（6V）、开关和带夹子的导线若干外，还需选用的其它器材有         （填选项前字母）（2）在虚线方框中画出实验电路图；

   （3）根据表格中数据在坐标纸上画出铅笔芯的I-U图线．

；