
题目列表(包括答案和解析)

A.杆的速度最大值为![]()
B.流过电阻R的电量为![]()
C.恒力F做的功与摩擦力做的功之和等于杆动能的变化量
D.恒力F做的功与安培力做的功之和大于杆动能的变化量
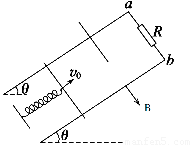
(19分)如图所示,固定的光滑金属导轨间距为d,导轨电阻不计,上端a、b间接有阻值为R的电阻,导轨平面与水平面的夹角为θ,且处在磁感应强度大小为B、方向垂直于导轨平面向下的匀强磁场中。质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上。初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0。整个运动过程中导体棒始终与导轨垂直并保持良好接触。已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行。
(1)求初始时刻通过电阻R的电流I大小和方向;
(2)当导体棒第一次回到初始位置时,速度变为v,求此时导体棒的加速度大小a;
(3)若导体棒最终静止时弹簧的弹性势能为Ep,求导体棒从开始运动直到停止的过程中,整个电路产生的焦耳热Q。
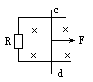
如下图所示,固定于水平绝缘面上的平行金属导轨不光滑,除R外其它电阻均不计,垂直导轨平面有一匀强磁场,当质量为m的金属棒cd在水平力F作用下由静止向右滑动过程中,下列说法中正确的是
[ ]
A.水平力F对cd所做功等于电路中产生的电能.
B.只有在cd棒做匀速运动时,F对cd棒做的功才等于电路中产生的电能
C.无论cd棒作何种运动,它克服磁场力做的功一定等于电路中产生的电能
D.R两端电压始终小于cd棒中感应电动势的值.
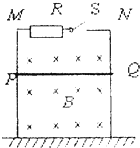 平行金属导轨MN竖直放置于绝缘水平地板上,如右图所示,金属杆PQ可以紧贴导轨无摩擦滑动,导轨间除固定电阻R以外,其它部分电阻不计,匀强磁场B垂直穿过导轨平面,以下有两种情况:第1次,先闭合开关S,然后从图中位置由静止释放PQ,经一段时间后PQ匀速到达地面;第2次,先从同一高度由静止释放PQ,当PQ下滑一段距离后突然闭合开关S,最终PQ也匀速到达了地面.设上述两种情况PQ由于切割磁感线产生的电能分别为W1、W2,则可以判定( )
平行金属导轨MN竖直放置于绝缘水平地板上,如右图所示,金属杆PQ可以紧贴导轨无摩擦滑动,导轨间除固定电阻R以外,其它部分电阻不计,匀强磁场B垂直穿过导轨平面,以下有两种情况:第1次,先闭合开关S,然后从图中位置由静止释放PQ,经一段时间后PQ匀速到达地面;第2次,先从同一高度由静止释放PQ,当PQ下滑一段距离后突然闭合开关S,最终PQ也匀速到达了地面.设上述两种情况PQ由于切割磁感线产生的电能分别为W1、W2,则可以判定( )| A、W1>W2 | B、W1=W2 | C、W1<W2 | D、以上结论都不正确 |
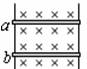
如下图所示,竖直放置的两光滑平行金属导轨放置于垂直于导轨向里的匀强磁场中,两根质量相同的金属棒a、b与导轨接触良好,且可沿导轨自由滑动。先固定a棒、释放b棒,当b棒的速度达到10m/s时,再释放a棒,经过1s时间a棒的速度达到12m/s,则此时金属棒b的速度为(g取10m/s2)
A.12m/s
B.18m/s
C.20m/s
D.22m/s
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com