
题目列表(包括答案和解析)
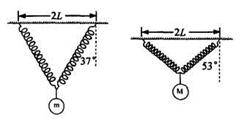
如图所示,将两根劲度系数均为k、原长均为L的轻弹簧,一端固定与水平天花板上相距为2L的两点,另一端共同连接一质量为m的物体,平衡时弹簧与竖直方向的夹角为37°。若将物体的质量变为M,平衡时弹簧与竖直方向的夹角为53°(sin37°=0.6),则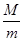 等于
等于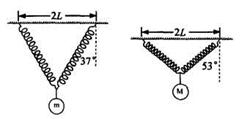
A.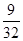 | B.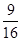 | C.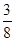 | D.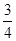 |
如图所示,将两根劲度系数均为k、原长均为L的轻弹簧,一端固定与水平天花板上相距为2L的两点,另一端共同连接一质量为m的物体,平衡时弹簧与竖直方向的夹角为37°。若将物体的质量变为M,平衡时弹簧与竖直方向的夹角为53°(sin37°=0.6),则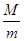 等于
等于
A.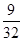 B.
B.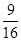 C.
C.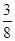 D.
D.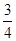
 等于
等于
A. | B. | C. | D. |
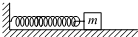 一劲度系数为k的轻质弹簧一端固定,另一端与质量为m的滑块相连.滑块在光滑水平面上做简谐运动,周期为T,振幅为A.滑块从最大位移向平衡位置运动的过程中,在求弹簧弹力的冲量大小时,有以下两种不同的解法: 一劲度系数为k的轻质弹簧一端固定,另一端与质量为m的滑块相连.滑块在光滑水平面上做简谐运动,周期为T,振幅为A.滑块从最大位移向平衡位置运动的过程中,在求弹簧弹力的冲量大小时,有以下两种不同的解法:
|
| 解法一 | 解法二 |
由于弹簧的弹力F与位移x成正比,所以甲同学先求出0~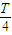 内的平均弹力 内的平均弹力 = =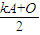 由于运动时间是 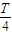 ,所以 ,所以I= 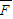 ? ? = =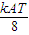 | 乙同学查阅资料后得到弹性势能的表达式是:Ep= kx2(x为弹簧的形变量). kx2(x为弹簧的形变量).设滑块到达平衡位置时的速度为v,根据机械能守恒定律:  kA2= kA2= mv2 mv2所以:v=A 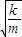 又根据动量定理:I=mv-O=A 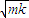 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com