如图所示，光滑水平面上，质量为m的小球A和质量为

1

3

m的小球B通过轻质弹簧相连并处于静止状态，此时弹簧处于原长：质量为m的小球C以初速度v₀沿AB连线向右匀速运动，并与小球A发生弹性正碰，从此时起到弹簧下次恢复到原长的过程中，弹簧的最大弹性势能．小球B的最大速度分别为（　　）

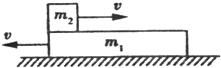如图所示，光滑水平面上，质量为m_l的足够长的木板向左匀速运动．t=0时刻，质量为m₂的木块从木板的左端向右以与木板相同大小的速度滑上木板．t₁时刻，木块和木板相对静止，共同向左匀速运动，以v₁和a₁表示木板的速度和加速度，以v₂和a₂表示木块的速度和加速度，以向左为正方向．则下列图中正确的是（　　）

如图所示，光滑水平面上，质量为2m的小球B连接着轻质弹簧、处于静止状态；质量为m的小球A以速度v₀向右匀速运动，接着逐渐压缩弹簧并使B运动，过一段时间后，A与弹簧分离．设小球A、B与弹簧相互作用过程中无机械能损失，弹簧始终处于弹性限度以内．
（1）求当弹簧被压缩到最短时，弹簧的弹性势能E．
（2）若开始时在小球B的右侧某位置固定一块挡板（图中未画出），在小球A与弹簧分离前使小球B与挡板发生正撞，并在碰后立刻将挡板撤走．设小球B与固定挡板的碰撞时间极短，碰后小球B的速度大小不变、但方向相反．设此后弹簧性势能的最大值为E_m，求E_m可能值的范围．

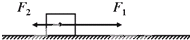如图所示，光滑水平面上，质量为m=4kg的静止木块受到方向相反的大小分别为F₁=6N、F₂=3N的水平恒力作用，求
（1）木块运动位移l₁=3m的过程中克服F₂做的功
（2）木块运动位移l₂=6m时速度v．