解析　(1)设木板第一次上升过程中，物块的加速度为a_物块，由牛顿第二定律kmgsin θ－mgsin θ＝ma_物块

解得a_物块＝(k－1)gsin θ，方向沿斜面向上

(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v₁

由机械能守恒得：×2mv＝2mgH

解得v₁＝

设木板弹起后的加速度为a_板，由牛顿第二定律得：

a_板＝－(k＋1)gsin θ

木板第一次弹起的最大路程s₁＝＝

木板运动的路程s＝＋2s₁＝

(3)设物块相对木板滑动距离为L

根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgLsin θ

摩擦力对木板及物块做的总功W＝－kmgLsin θ

解得W＝－

答案　(1)(k－1)gsin θ；方向沿斜面向上

(2)　(3)－

解析　(1)小球从曲面上滑下，只有重力做功，由机械能守恒定律知：

mgh＝mv                                                       ①

得v₀＝＝ m/s＝2 m/s.

(2)小球离开平台后做平抛运动，小球正好落在木板的末端，则

H＝gt²                                                                                                                                                      ②

＝v₁t                                                                                                                ③

联立②③两式得：v₁＝4 m/s

设释放小球的高度为h₁，则由mgh₁＝mv

得h₁＝＝0.8 m.

(3)由机械能守恒定律可得：mgh＝mv²

小球由离开平台后做平抛运动，可看做水平方向的匀速直线运动和竖直方向的自由落体运动，则：

y＝gt²                                                                                                                                                       ④

x＝vt                                                                                                                       ⑤

tan 37°＝                                                                                                          ⑥

v_y＝gt                                                                                                                      ⑦

v＝v²＋v                                                       ⑧

E_k＝mv                                                      ⑨

由④⑤⑥⑦⑧⑨式得：E_k＝32.5h                                                                       ⑩

考虑到当h>0.8 m时小球不会落到斜面上，其图象如图所示

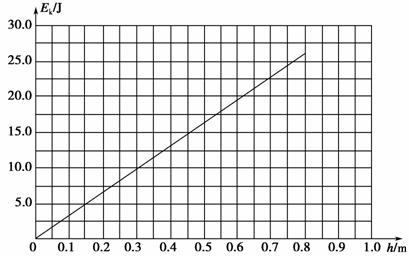
答案　(1)2 m/s　(2)0.8 m　(3)E_k＝32.5h　图象见解析

人在平板车上用水平恒力拉绳使重物能靠拢自己，如图所示，人相对车始终不动，重物与平板车之间，平板车与地面之间均无摩擦．设开始拉重物时车和重物都是静止的，车和人的总质量为M＝100 kg，重物质量m＝50 kg，拉力F＝20 N，重物在车上向人靠拢了3 m．求：

(1)车在地面上移动的距离．

(2)这时车和重物的速度．

【解析】：(1)设重物在车上向人靠拢L＝3 m，车在地面上移动距离为x，依题意有m(L－x)＝Mx

整理得：x＝1 m

(2)人和车的加速度为a＝＝＝2 m/s²

则人和车在地面上移动1 m时的速度为

v＝＝2 m/s

此时物体的对地速度为v_物，依据mv_物＝Mv

得v_物＝4 m/s

 

设宇航员在某行星上从高32 m处自由释放一重物，测得在下落最后1 s内所通过的距离为14 m，则重物下落的时间是多少？该星球表面的重力加速度为多大？

【解析】：设物体下落的时间为t，星球表面的重力加速度为g，则h＝gt²①

h－14＝g(t－1)²②

由题意知h＝32 m，由①②解得t₁＝4 s，t₂＝ s(舍去)，所以t＝t₁＝4 s，g＝4 m/s².

 

(1)设宇宙射线粒子的能量是其静止能量的k倍．则粒子运动时的质量等于其静止质量的________倍，粒子运动速度是光速的________倍．

(2)某实验室中悬挂着一弹簧振子和一单摆，弹簧振子的弹簧和小球(球中间有孔)都套在固定的光滑竖直杆上．某次有感地震中观察到静止的振子开始振动4.0s后，单摆才开始摆动．此次地震中同一震源产生的地震纵波和横波的波长分别为10 km和5.0 km，频率为1.0 Hz.假设该实验室恰好位于震源的正上方，求震源离实验室的距离．

【解析】：(1)以速度v运动时的能量E＝mv²，静止时的能量为E₀＝m₀v²，依题意E＝kE₀，故m＝km₀；

由m＝，解得v＝c.

(2)地震纵波传播速度为：v_p＝fλ_p

地震横波传播速度为：v_s＝fλ_s

震源离实验室距离为s，有：s＝v_pt

s＝v_s(t＋Δt)，解得：s＝＝40 km.