
题目列表(包括答案和解析)
| 1 |
| 2 |

| . |
| OE |

 的长度;
的长度;
 的长度;
的长度;
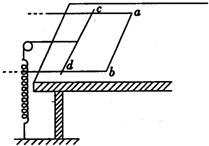 (2013?河南模拟)如图所示,在一光滑水平的桌面上,放置一质量为M,宽为L的足够长“U”型框架,其ab部分电阻为R,框架其它部分的电阻不计.垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,棒通过细线跨过一定滑轮与劲度系数为k的另一端固定的轻弹簧相连.开始弹簧处于自然状态,框架和棒均静止.现在让框架在大小为2μmg的水平拉力作用下,向右做加速运动,引起棒的运动可看成是缓慢的.水平桌面位于竖直向上的匀强磁场中,磁感应强度为B.问:
(2013?河南模拟)如图所示,在一光滑水平的桌面上,放置一质量为M,宽为L的足够长“U”型框架,其ab部分电阻为R,框架其它部分的电阻不计.垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,棒通过细线跨过一定滑轮与劲度系数为k的另一端固定的轻弹簧相连.开始弹簧处于自然状态,框架和棒均静止.现在让框架在大小为2μmg的水平拉力作用下,向右做加速运动,引起棒的运动可看成是缓慢的.水平桌面位于竖直向上的匀强磁场中,磁感应强度为B.问:| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com