
题目列表(包括答案和解析)
 在用单摆测重力加速度的实验中:
在用单摆测重力加速度的实验中:| y2-y1 |
| x2-x1 |
| y2-y1 |
| x2-x1 |
 在用单摆测重力加速度的实验中:
在用单摆测重力加速度的实验中:| x2-x1 |
| y2-y1 |
| x2-x1 |
| y2-y1 |
在用单摆测重力加速度的实验中:
(1)实验时必须控制摆角,若摆长为1.2m,则要将摆球拉至离平衡位置约_______m处释放.
(2)某同学实验时改变摆长,测出几组摆长L和对应的周期T的数 据,作出T2—L图线,如图所示.利用图线上任两点A、B的坐标(x1,y1)、(x2,y2),便可求得重力加速度g= .
(3)作T2—L图线解决物理问题,可以提示我们:若摆球的质量分布不均匀,对测量结果将__________________________________.
在用单摆测重力加速度的实验中:
(1)实验时必须控制摆角,若摆长为1.2m,则要将摆球拉至离平衡位置约_______m处释放.
(2)某同学实验时改变摆长,测出几组摆长L和对应的周期T的数 据,作出T2—L图线,如图所示.利用图线上任两点A、B的坐标(x1,y1)、(x2,y2),便可求得重力加速度g= .
(3)作T2—L图线解决物理问题,可以提示我们:若摆球的质量分布 不均匀,对测量结果将__________________________________.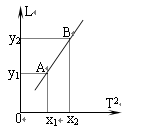
在用单摆测重力加速度的实验中:
(1)实验时必须控制摆角,若摆长为1.2m,则要将摆球拉至离平衡位置约_______m处释放.
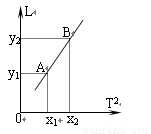
(2)某同学实验时改变摆长,测出几组摆长L和对应的周期T的数 据,作出T2—L图线,如图所示.利用图线上任两点A、B的坐标(x1,y1)、(x2,y2),便可求得重力加速度g= .
(3)作T2—L图线解决物理问题,可以提示我们:若摆球的质量分布 不均匀,对测量结果将__________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com