
题目列表(包括答案和解析)



如图,质量为m1的物体A 经一轻质弹簧与下方地面上的质量为m2的物体B 相连,弹簧的劲度系数为k , A .B 都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体A ,另一端连一轻挂钩。开始时各段绳都处于伸直状态,A 上方的一段绳沿竖直方向。现在挂钩上挂一质量为m3的物体C 并从静止状态释放,已知它恰好能使B 离开地面但不继续上升。若将C 换成另一个质量为(m1+ m3)的物体D ,仍从上述初始位置由静止状态释放,则这次B 刚离地时D的速度的大小是多少?已知重力加速度为g 。
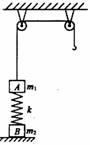
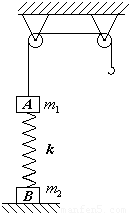 如图,质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为m3的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将C换成另一个质量为(m1十m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度为g.
如图,质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为m3的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将C换成另一个质量为(m1十m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度为g.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com