在图所示的两端开口的“U”形管中，盛有同种液体，并用阀门K将液体隔成左、右两部分，左边液面比右边液面高．现打开阀门K，从打开阀门到两边液面第一次平齐的过程中，液体向外放热为Q，内能变化量为ΔU，动能变化量为ΔE_k；大气对液体做功为W₁，重力做功为W₂，液体克服阻力做功为W₃，由功能关系可得

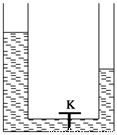
①W₁＝0  ②W₂－W₃＝ΔE_k

③W₂－W₃＝Q＝ΔU  ④W₃－Q＝ΔU

其中，正确的是(  )

A．①②③                  B．①②④

C．②③                    D．①③

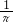物体因绕轴转动时而具有的动能叫转动动能．转动动能的大小与角速度大小有关，为了探究转动动能的大小与角速度之间的定量关系，某同学设计了下列一个实验，即研究砂轮的转动．先让砂轮由电动机带动作匀速转动并测出其角速度ω，然后让砂轮脱离动力，由于克服轮边缘的摩擦阻力做功，砂轮最后会停下来，测出砂轮开始脱离动力到停止转动的圈数n，实验中得到几组n和ω的数值见下表：（砂轮直径d=10cm，转轴间摩擦力大小 f= N）

n	5	20	80	180	320
ω（rad/s）	0.5	1	2	3	4
Ek（J）	______	______	______	______	______

（1）根据功能关系，请你帮他计算出砂轮每次脱离动力时的转动动能，并填入表格内；
（2）利用实验数据，请你帮他确定此砂轮的转动动能与角速度大小间的定量关系式是______．

如下图所示，将轻弹簧放在光滑的水平凹形轨道上，一端与轨道的A端固定，另一端正好在轨道的B端处，轨道固定在水平桌面的边缘上，桌边悬一重锤．根据平抛运动的规律和功能关系的相关知识，可利用该装置找出弹簧压缩时具有的弹性势能与压缩量之间的关系．

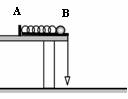
   （1）为完成实验，还需下面哪些器材     （    ）

A.秒表   B.刻度尺   C. 白纸   D. 复写纸   E. 天平  F.弹簧秤

   （2）如果在实验中，得到弹簧压缩量x和小球离开桌面后的水平位移s的一些数据如下表，经你的推导分析，得到的实验结论是：                                   。

   （3）为提高实验结果的准确程度，请写出至少两条可以提高实验结果准确程度的有益的建议：                                                       。

（10分）物体因绕轴转动时而具有的动能叫转动动能。转动动能的大小与角速度大小有关，为了探究转动动能的大小与角速度之间的定量关系，某同学设计了下列一个实验，即研究砂轮的转动。先让砂轮由电动机带动作匀速转动并测出其角速度ω，然后让砂轮脱离动力，由于克服轮边缘的摩擦阻力做功，砂轮最后停下来，测出砂轮开始脱离动力到停止转动的圈数n，实验中得到几组n和ω的数值见下表：（砂轮直径d=10cm，转轴间摩擦力大小N）

（1）根据功能关系，请你帮他计算出砂轮每次脱离动力时的转动动能，并填入表格内；

（2）利用实验数据，请你帮他确定此砂轮的转动动能与角速度大小定量关系式 是           。