
题目列表(包括答案和解析)
| t |
| n |
| 4π2l |
| T2 |
| θ |
| 2 |
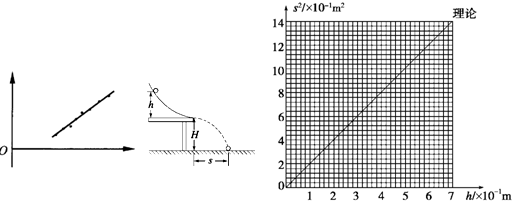
| h(10-1m) | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| s2(10-1m2) | 2.62 | 3.89 | 5.20 | 6.53 | 7.78 |
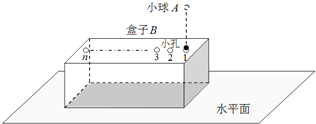
如图所示,A为位于一定高度处的质量为m的小球,B为位于水平地面上的质量为M的长方形空心盒子,盒子足够长,且M = 2m,盒子与地面间的动摩擦因数![]() =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.

如图所示,A为位于一定高度处的质量为m的小球,B为位于水平地面上的质量为M的长方形空心盒子,盒子足够长,且M = 2m,盒子与地面间的动摩擦因数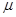 =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:

(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.
如图所示,A为位于一定高度处的质量为m的小球,B为位于水平地面上的质量为M的长方形空心盒子,盒子足够长,且M = 2m,盒子与地面间的动摩擦因数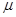 =0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
=0.2.盒内存在着某种力场,每当小球进入盒内,该力场将同时对小球和盒子施加一个大小为F=Mg、方向分别竖直向上和向下的恒力作用;每当小球离开盒子,该力F同时立即消失.盒子的上表面开有一系列略大于小球的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以v=1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v0=6m/s的速度向右滑行.取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求: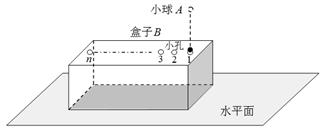
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com