（1）①甲、乙、丙、丁四位同学在使用不同精度的游标卡尺和螺旋测微器测量物体的长度时，分别测量的结果如下：
甲同学：使用游标为50分度的卡尺，读数为12.045cm
乙同学：使用游标为10分度的卡尺，读数为12.04cm
丙同学：使用游标为20分度的卡尺，读数为12.045cm
丁同学：使用精度为“0.01mm”的螺旋测微器，读数为12.040mm
从这些实验数据中可以看出读数肯定有错误的是同学．
②如图甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮悬挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图乙ab虚线所示，再增加一个钩码后，P点对应刻度如图乙cd虚线所示，已知每个钩码质量为50g，重力加速度g=9.80m/s²，则被测弹簧的劲度系数为N/m，挂三个钩码时弹簧的形变量为cm．

（2）为了确定一卷金属漆包线的长度，可通过测定其电阻值和去掉漆层后金属导线的直径来实现．现仅有下列器材：
A、待测漆包线：电阻值R_L在40～50Ω之间，其材料的电阻率ρ=1.7×10^-8Ω?m；
B、毫安表mA：量程1mA，内阻R_A=50Ω；  C、电压表V：量程6V，内阻R_V=4kΩ；
D、电源E：电动势约9V，内阻不计；     E、滑动变阻器R：阻值范围0～10Ω；
F、螺旋测微器，开关S，导线若干．
①若这卷漆包线的电阻值为R_L，金属导线的直径为d，金属电阻率为ρ，则这卷漆包线的长度L=（用R_L、d、ρ表示）．
②为了尽可能准确地测定R_L，要求两电表指针偏转至少达到满刻度的一半．同学们设计了以下四种不同的电路，其中合理的是．

③实验中测得d=0.200mm，按合理的接法测量时，毫安表和电压表的示数如图丙所示，则毫安表的读数为 mA，电压表的读数 V，可求得该卷漆包线的长度 L= m．

2008年 8月19日晚，北京奥运会男子体操单杠决赛在国家体育馆举行，中国四川小将邹凯（如图）以高难度的动作和出色的发挥以16.20分夺得金牌，小将邹凯做“单臂大回环”时，用一只手抓住单杠，伸展身体，以单杠为轴作圆周运动．此过程中，运动员的重心到单杠的距离为R，忽略空气阻力，则下列说法正确的是（　　）

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应时间△t的比值定义为角加速度β．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D…为计数点，相邻两计数点间有四个点未画出）
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，圆盘停止转动和打点，取下纸带，进行测量．（计算结果 保留3位有效数字）．
（1）用20分度的游标卡尺测得圆盘的直径如图乙所示，圆盘的半径r为．cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为rad/s；
（3）纸带运动的加速度大小为m/s²，圆盘转动的角加速度大小为．rad/s²．

一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应之间△t的比值定义为角加速度β（即ρ=

△?

△t

）．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D…为计数点，相邻两计数点间有四个点未画出）
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，停止转动和打点，取下纸带，进行测量．
（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为rad/s；
（3）纸带运动的加速度大小为m/s²，圆盘转动的角加速度大小为rad/s²；
（4）如果实验测出的角加速度值偏大，其原因可能是（至少写出1条）．

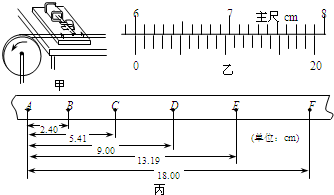一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应之间△t的比值定义为角加速度β（即β=

△ω

△t

）．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D…为计数点，相邻两计数点间有四个点未画出）
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，停止转动和打点，取下纸带，进行测量．
（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为 rad/s；
（3）纸带运动的加速度大小为m/s²，圆盘转动的角加速度大小为rad/s²．
▲请注意：本题（2）、（3）问中的结果均要求保留2位有效数字．