水上滑梯可简化成如图5－2－19所示的模型，斜槽AB和水平槽BC平滑连接，斜槽AB的竖直高度H＝6.0 m，倾角θ＝37°.水平槽BC长d＝2.0 m，BC面与水面的距离h＝0.80 m，人与AB、BC间的动摩擦因数均为μ＝0.10.取重力加速度g＝10 m/s²，cos 37°＝0.8，sin 37°＝0.6.一小朋友从滑梯顶端A点无初速地自由滑下，求：

(1)小朋友沿斜槽AB下滑时加速度的大小a；

(2)小朋友滑到C点时速度的大小v；

(3)在从C点滑出至落到水面的过程中，小朋友在水平方向位移的大小s.

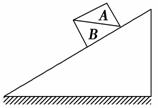
如图2－3－19所示，A和B两物块的接触面是水平的，A与B保持相对静止一起沿固定斜面匀速下滑，在下滑过程中B的受力个数为                                                 (　　)．

A．3个                 B．4个

C．5个                 D．6个

斜面长度为4 m，一个尺寸可以忽略不计的滑块以不同的初速度v₀从斜面顶端沿斜面下滑时，其下滑距离x与初速度二次方v的关系图象(即x－v图象)如图1－3－19所示．

(1)求滑块下滑的加速度大小．

(2)若滑块下滑的初速度为5.0 m/s，则滑块沿斜面下滑的时间为多长？

如图6－3－19所示，用长L＝0.50 m的绝缘轻质细线，把一个质量m＝1.0 g带电小球悬挂在均匀带等量异种电荷的平行金属板之间，平行金属板间的距离d＝5.0 cm，两板间电压U＝1.0×103 V．静止时，绝缘细线偏离竖直方向θ角，小球偏离竖直线的距离a＝1.0 cm.取g＝10 m/s2.则下列说法正确的是             (　　)．

A．两板间电场强度的大小为2.0×104 V/m

B．小球带的电荷量为1.0×10－8 C

C．若细线突然被剪断，小球在板间将做类平抛运动

D．若细线突然被剪断，小球在板间将做匀加速直线运动

．由实验测得某弹簧的弹力F与长度L的关系如图2－3－19所示．则该弹簧的原长L为多少，劲度系数k为多少？

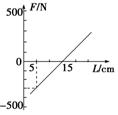
图2－3－19

【解析】：当弹簧的弹力为零时，弹簧处于原长状态，由图可以知道L＝15 cm.当弹簧长度为5 cm时弹力大小为300 N，对应弹簧的压缩量为10 cm，由胡克定律F＝k·x得：

k＝＝＝30 N/cm＝3×10³ N/m.