(12分)如图8所示，在倾角为θ的光滑斜面上端系有一劲度系数 为k的轻质弹簧，弹簧下端连一个质量为m的小球，球被一垂直于斜面的挡板A挡住，此时弹簧没有形变．若挡板A以加速度a (a＜gsinθ)沿斜面向下匀加速运动，问：                         

(1)小球向下运动多少距离时速度最大？

(2)从开始运动到小球与挡板分离所经历的时间为多少？

图8

如图所示，在倾角为的光滑斜面上，有一根长为L=0.8 m的细绳，一端固定在O点，另一端系一质量为m＝0. 2 kg的小球，沿斜面做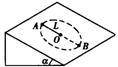圆周运动，若要小球能通过最高点A，则小球在最低点B的最小速度是（ ）

A．2 m/s  B．m/s

C．m/s    D．m/s

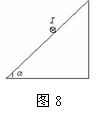在倾角为α的光滑斜面上，置一通有电流I，长L，质量为m的导体棒，如图8所示，试问

（1）欲使棒静止在斜面上，外加匀强磁场的磁感应强度B的最小值和方向.

(2)欲使棒静止在斜面上且对斜面无压力，外加匀强磁场的磁感应强度B的大小和方向. (3)分析棒有可能静止在斜面上且要求B垂直L，应加外磁场的方向范围.

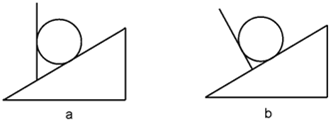
如图8-6所示，在倾角为α的光滑斜面上，垂直纸面放置一根长为L，质量为m的直导体棒．当导体棒中的电流I垂直纸面向里时，欲使导体棒静止在斜面上，可加一平行于纸面的匀强磁场，当外加匀强磁场的磁感应强度B的方向由垂直斜面向上沿逆时针转至水平向左的过程中，下列关于B的大小变化的说法中，正确的是(　　)．

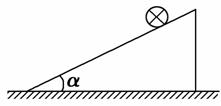
图8-6

A．逐渐增大                                                         B．逐渐减小

C．先减小后增大                                                  D．先增大后减小