练习册

  • 练习册
  • 试题
    平抛运动 (1)定义:将一物体水平抛出.物体只在 重力 作用下的运动. (2)性质:加速度为g的匀变速 曲线 运动.运动过程中水平速度 不变 .只是竖直速度不断 增大 .合速度大小.方向时刻 改变 . (3)研究方法:将平抛运动分解为水平方向的 匀速直线 运动和竖直方向的 自由落体 运动.分别研究两个分运动的规律.必要时再用运动合成方法进行合成. (4)规律: 设平抛运动的初速度为v0.建立坐标系如图. 速度.位移: 水平方向:vx＝v0.x＝v0t 竖直方向:vy＝gt.y＝gt2 合速度大小(t秒末的速度): vt＝ 方向:tan φ＝ 合位移大小(t秒末的位移):s＝ 方向:tan θ＝ 所以tan φ＝2tan θ 运动时间:由y＝gt2得t＝(t由下落高度y决定). 轨迹方程:y＝ (在未知时间情况下应用方便). 可独立研究竖直分运动: a.连续相等时间内竖直位移之比为1∶3∶5∶-∶(2n-1)(n＝1,2,3-) b.连续相等时间内竖直位移之差为Δy＝gt2 一个有用的推论: 平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半. 【查看更多】

     

    题目列表(包括答案和解析)

    为了研究平抛物体的运动，可做下面的实验：如图甲所示，用小锤打击弹性金属片，B球就水平飞出，同时A球被松开，做自由落体运动，两球同时落到地面；如图乙所示的实验：将两个完全相同的斜滑道固定在同一竖直面内，最下端水平．把两个质量相等的小钢球从斜面的同一高度由静止同时释放，滑道2与光滑水平板吻接，则将观察到的现象是球1落到水平木板上击中球2，这两个实验说明（　　）

    查看答案和解析>>

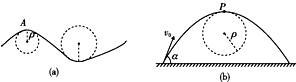
    一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替，如图（a）所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆．在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径．现将一物体沿与水平面成α角的方向以速度v0抛出，如图（b）所示，则在其轨迹最高点P处的曲率半径是（　　）精英家教网
    A、
    v
    2
    0
    g
    B、
    v
    2
    0
    sin2α
    g
    C、
    v
    2
    0
    cos2α
    g
    D、
    v
    2
    0
    cos2α
    gsinα

    查看答案和解析>>

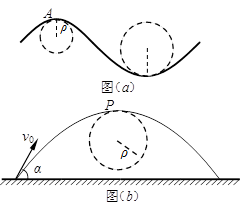
    一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替。如图（a）所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径。现将一物体沿与水平面成α角的方向已速度υ0抛出，如图（b）所示。则在其轨迹最高点P处的曲率半径是

    A．              B．  

    C．        D．

    查看答案和解析>>

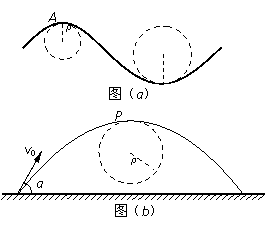
    一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替．如图4－3－12甲所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径．现将一物体沿与水平面成α角的方向以速度v0抛出，如图4－3－12乙所示．则在其轨迹最高点P处的曲率半径是                                                                      (　　)．

     　

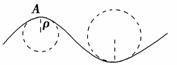
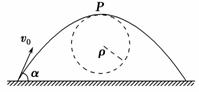
    甲　　　　　　　　　　　 　　乙　

    图4－3－12

    A.             B.           C.                 D.

    查看答案和解析>>

    一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替。如图（a）所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径。现将一物体沿与水平面成α角的方向已速度υ0抛出，如图（b）所示。则在其轨迹最高点P处的曲率半径是

    A．     B．   C．    D．

     

    查看答案和解析>>


    同步练习册答案