
题目列表(包括答案和解析)
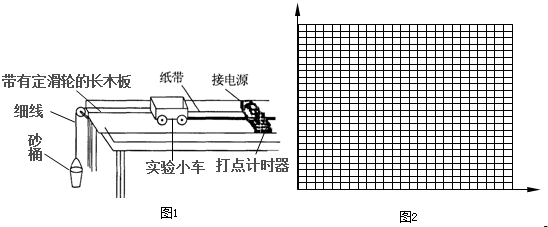
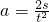 计算;b.根据
计算;b.根据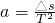 利用逐差法计算.两种方案中,你认为选择方案______比较合理,而另一种方案不合理的理由是______.
利用逐差法计算.两种方案中,你认为选择方案______比较合理,而另一种方案不合理的理由是______.| 物理量 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| m砂(kg) | 0.010 | 0.020 | 0.030 | 0.040 | 0.050 | 0.060 |
| F(N) | 0.098 | 0.196 | 0.294 | 0.392 | 0.490 | 0.588 |
| a(m/s2) | 0.196 | 0.390 | 0.718 | 0.784 | 0.990 | 1.176 |
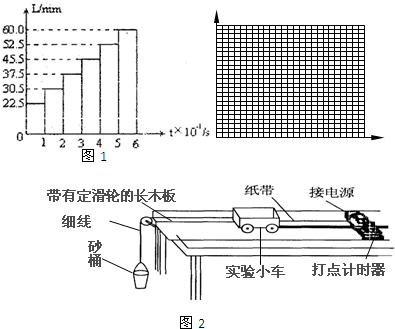
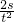 计算;B、根据a=
计算;B、根据a=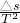 利用逐差法计算.
利用逐差法计算.| 次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 |
| m砂和桶(kg) | 0.010 | 0.020 | 0.030 | 0.040 | 0.050 | 0.060 |
| a(m/s2) | 0.196 | 0.390 | 0.718 | 0.784 | 0.990 | 1.176 |
| |||||||||||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com