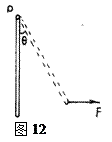
如图12所示粗细均匀的木棒长为L，质量为M ，可绕固定转动轴O自由转动，现用水平力F作用于木棒的下端将木棒从竖直位置缓慢拉起，并转过θ角度，则在拉起的过程中，拉力F做的功为多少？

 某同学解法为：

木棒与竖直位置成θ时，木棒所受的力矩平衡   Mg Lsinθ/2= F Lcosθ，

得到F=Mgtgθ/2

从竖直位置缓慢拉起的过程中，  拉力F从0变化到Mgtgθ/2，

拉力F的平均值=Mgtgθ/4          

拉力作用点在力F方向上的位移是    S=L sinθ

根据W=FS     解得 ：拉力F 做的功：W_F= Mg L sinθtgθ/4

所以在拉起的过程中，拉力F做的功为W_F=Mg L sinθtgθ/4 ，

你认为他的解法是否正确？若正确，请说明理由；若错误，也请说明理由，并且解出正确的结果。

如图所示，一根重G=40N的均匀木棒AB，A端用细绳吊在固定点O上，今用水平力F=30N作用于B端，棒平衡时，下面说法正确的是  （    ）

A、绳子拉力T一定大于G     

B、力F增加时，绳与竖直方向的夹角α增加

C、杆AB与竖直夹角必等于绳与竖直方向的夹角α

D、力F足够大时，细绳可在水平方向上