
题目列表(包括答案和解析)
如图所示,不计重力的细绳AB与竖直墙夹角为60°,轻杆BC与竖直墙夹角为30°,杆可绕C自由转动,若细绳能承受的最大拉力为200 N,转杆能承受的最大压力为300 N,则在B点最多能挂多重的物体?

 如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,C的质量为4m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑至速度最大时A恰好离开地面.求:
如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,C的质量为4m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑至速度最大时A恰好离开地面.求: 如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆BO上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳AB段保持水平.C端挂一重物,BO与竖直方向θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )
如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆BO上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳AB段保持水平.C端挂一重物,BO与竖直方向θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )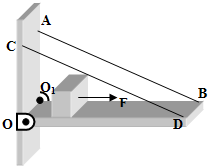 如图所示,质量不计、长度1米的轻质薄木板BDOO1被铰链和轻质细绳AB、CD水平地固定在竖直墙壁上,AB、CD与水平木板之间的夹角为30度,一重量为10牛顿的木块(可视为质点)置于木板的左端,木块与木板之间的摩擦系数为0.2,现对物块施加一水平向右的拉力F,F=7N,两根绳子各自能承受的最大拉力为9N,问:
如图所示,质量不计、长度1米的轻质薄木板BDOO1被铰链和轻质细绳AB、CD水平地固定在竖直墙壁上,AB、CD与水平木板之间的夹角为30度,一重量为10牛顿的木块(可视为质点)置于木板的左端,木块与木板之间的摩擦系数为0.2,现对物块施加一水平向右的拉力F,F=7N,两根绳子各自能承受的最大拉力为9N,问: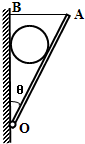 如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问:
如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com