如图8-5所示.A B和C D为半径为R=l m的1/4圆弧形光滑轨道.B C为一段长2m的水平轨道．质量为2 kg的物体从轨道A端由静止释放.若物体与水平轨道B C间的动摩擦因数为0.1.求:(l)——青夏教育精英家教网—

如图8-5所示.A B和C D为半径为R=l m的1/4圆弧形光滑轨道.B C为一段长2m的水平轨道．质量为2 kg的物体从轨道A端由静止释放.若物体与水平轨道B C间的动摩擦因数为0.1.求:(l)物体第1次沿C D弧形轨道可上升的最大高度．(2)物体最终停下来的位置与B点的距离．(g=10 m/s2) 【查看更多】

题目列表(包括答案和解析)

如图8-5所示，一段导线abcd弯成半径为R、圆心角为90°的部分扇形形状，置于磁感应强度大小为B的匀强磁场中，且与磁场方向(垂直于纸面向里)垂直．线段ab和cd的长度均为.流经导线的电流为I，方向如图8-5中箭头所示．则导线abcd所受到的安培力为(　　)．

图8-5

A．方向沿纸面向上，大小为

B．方向沿纸面向上，大小为

C．方向沿纸面向下，大小为

D．方向沿纸面向下，大小为

查看答案和解析>>

如图1为“碰撞中的动量守恒”实验装置示意图

（1）入射小球1与被碰小球2直径相同，均为d，它们的质量相比较，应是m₁

＞

m₂．
（2）为了保证小球做平抛运动，必须调整斜槽

其末端切线水平

．
（3）某次实验中在纸上记录的痕迹如图2所示．测得OO′=1.00厘米，O′a=1.80厘米，ab=5.72厘米，bc=3.50厘米，入射球质量为100克，被碰小球质量是50克，两球直径都是1.00厘米，则入射球碰前落地点是纸上的

点，水平射程是

8.52

厘米，被碰小球的水平射程是

64.7

厘米．
（4）某同学改用图3所示装置，通过半径相同的A、B两球的碰撞来验证动量守恒定律．

①碰撞后B球的水平程应取为

66.0

cm．
②在以下选项中，哪些是本次实验必须进行的测量？
答：

ABD

（填选项号）．
（A）水平槽上未放B球时，测量A球落点位置到O点的距离
（B）A球与B球碰撞后，测量A球落点位置到O点的距离
（C）测量A球或B球的直径
（D）测量A球和B球的质量（或两球质量之比）
（E）测量G点相对于水平槽面的高度．

查看答案和解析>>

如图所示,质量为3.0 kg的小车以1.0 m/s的速度在光滑的水平面上向左运动,车上AD部分是表面粗糙的水平轨道,DC部分是

光滑圆弧,整个轨道都是由绝缘材料制成的,小车所在空间内有竖直向上的匀强电场和垂直纸面向里的匀强磁场,电场强度E为40 N/C,磁感应强度B为2.0 T.现有一质量为1.0 kg、带负电且电荷量为1.0×10^-2 C的滑块以8.0 m/s的水平速度向右冲上小车，当它通过D点时速度为5.0 m/s(滑块可视为质点，g取10 m/s²).(计算结果保留两位有效数字)

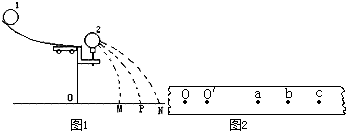
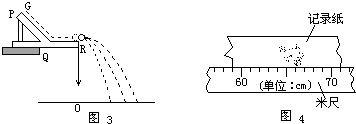
(1)求滑块从A到D的过程中，小车、滑块组成的系统损失的机械能；

(2)如果圆弧轨道半径为1.0 m，求滑块刚过D点时对轨道的压力；

(3)若滑块通过D点时，立即撤去磁场，要使滑块不冲出圆弧轨道，求此圆弧的最小半径.

查看答案和解析>>

如图所示是游乐场中过山车的实物图片，左图所示是过山车的简化模型图．在模型图中水平倾角都为α=37°，斜轨道AB、CD、EF与竖直光滑圆形（圆弧）轨道圆滑连接．B、C、D、E、F为对应的切点．其中两个圆轨道半径分别为R₁=6.0m和R₃=3.0m，中间圆弧轨道的半径为R₂．且两圆形轨道的最高点P、Q与A、D、E点平齐．现使小车（视作质点）从A点以一定的初速度沿斜面向下运动．已知斜轨道面与小车间的动摩擦因数为μ=1/24，g=10m/s²，sin37°=0.6，cos37°=0.8，tan18.5=1/3．问：
（1）若小车恰好能通过第一个圆形轨道的最高点P处，则其在A点的初速度v应为多大？
（2）若在（1）问情况下小车能安全到达E点，则能否安全通过第三个圆形轨道的Q点？
（3）若小车在A点的初速度为

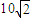m/s，且R₂=10m则小车能否安全通过整段轨道？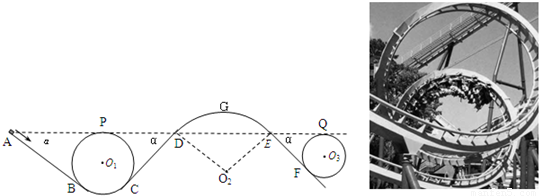

查看答案和解析>>

如图所示，宽h=2cm的有界匀强磁场的纵向范围足够大，磁感应强度的方向垂直纸面向内，现有一群正粒子从O点以相同的速率沿纸面不同方向进入磁场，若粒子在磁场中做匀速圆周运动的轨道半径均为r=5 cm，则（）

A．右边界：－4 cm<y<4 cm有粒子射出

B．右边界：y >4 cm和y<－4 cm有粒子射出

C．左边界：y >8 cm有粒子射出

D．左边界：0< y <8 cm有粒子射出

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学