
题目列表(包括答案和解析)
 如图所示,倾角为θ的斜劈,斜劈质量为M,始终静止.其斜面上静止着质量为m的物体,地面对斜劈的支持力为
如图所示,倾角为θ的斜劈,斜劈质量为M,始终静止.其斜面上静止着质量为m的物体,地面对斜劈的支持力为如图所示,倾角为 的斜面上OP段光滑,PQ段粗糙,
的斜面上OP段光滑,PQ段粗糙, 为滑块A与PQ段的摩擦因数且
为滑块A与PQ段的摩擦因数且 ,滑块A与水平顶面上的物块B保持相对静止从斜面上O点由静止开始下滑到Q的过程,B与A之间始终无相对滑动。则关于物块B在OP段和PQ段的受力情况,下列说法中正确的是
,滑块A与水平顶面上的物块B保持相对静止从斜面上O点由静止开始下滑到Q的过程,B与A之间始终无相对滑动。则关于物块B在OP段和PQ段的受力情况,下列说法中正确的是
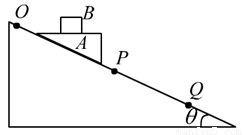
A.在OP段物块B仅受重力
B.在OP段物块B仅受重力和支持力
C.在PQ段A对B的支持力大于B的重力
D.在PQ段物块B受到水平向右的摩擦力
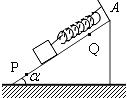
如图所示,倾角为![]() 的斜面上,放一质量为1kg的物体,用k=100N/m的弹簧平行于斜面吊着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体都会沿斜面滑动。若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小。(g=10m/s2)
的斜面上,放一质量为1kg的物体,用k=100N/m的弹簧平行于斜面吊着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体都会沿斜面滑动。若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小。(g=10m/s2)
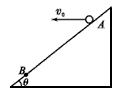
如图所示, 在倾角为θ的斜面上, 放一个质量为M的物体, 用细绳跨过定滑轮与质量为m的砝码连接. 物体与斜面间的动摩擦因数为μ, 绳的质量及它们间的摩擦均忽略不计. 则:
(1)要使物体M沿斜面向上作匀速运动, ![]() 的值应满足的条件是______.
的值应满足的条件是______.
(2)若m=0, 那么要使M沿斜面匀速下滑, 倾角θ应为_______.
![]()
![]()
[ ]




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com