练习册

  • 练习册
  • 试题
    如图1所示.质量均为的.两球之间系着一条不计质量的轻弹簧.放在光滑的水平面上.球紧靠墙壁.今用力将球向左推压弹簧.平衡后.突然将力撤去的瞬间.则 A.A球的加速度为 B.A球的加速度为零 C.B球的加速度为 D.B球的加速度为0 【查看更多】

     

    题目列表(包括答案和解析)

    如图甲所示，质量均为m的、可视为质点的两个带电小球A，B被固定在弯成90°角的绝缘轻杆两端，OA和OB的长度均为L，可绕过O点的、与纸面垂直的水平轴无摩擦的转动，空气的作用力不计。已知A球带电量qA=+q，B球带电量qB=+3q，绝缘轻杆、A和B组成的系统在竖直向下的匀强电场中处于平衡状态，杆OA与竖直方向的夹角θ=53°，静电力常量用K表示，sin53°=0.8，cos53°=0.6。试求：
    (1)竖直向下的匀强电场的场强E；
    (2)将带正电的、也可视为质点的小球C从无限远处缓慢地移入，使绝缘轻杆缓慢地转动，在小球C到轴O的正下方L处时。恰好使杆OA（与竖直方向的夹角θ=45°）处于平衡状态，如图乙所示，小球C带电量qC；
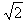    (3)在(2)的条件下，若已知小球C从无限远处缓慢地移到轴O的正下方L处的过程中，小球C克服匀强电场的电场力做功为W1，小球A，B，C之间的库仑力做功为W2，则在这个过程中匀强电场和小球A，B，C组成的整个系统的电势能变化量△W为多少？

    查看答案和解析>>

    如图1所示，光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mb=2ma，规定向右为正方向，A、B两球的动量均为6 kg·m/s，运动中两球发生碰撞，碰撞后A球的动量增量为-4 kg·m/s.则(　　)?

    图1

    A.左方是A球，碰撞后A、B两球速度大小之比为2∶5?

    B.左方是A球，碰撞后A、B两球速度大小之比为1∶10?

    C.右方是A球，碰撞后A、B两球速度大小之比为2∶5?

    D.右方是A球，碰撞后A、B两球速度大小之比为1∶10?

    查看答案和解析>>

    如图1所示，两个质量均为m的完全相同的金属球壳a与b，其壳层的厚度和质量分布均匀，将它们固定于绝缘支座上，两球心间的距离l为球半径的3倍.若使它们带上等量异种电荷，使其电荷量的绝对值均为Q，那么，a、b两球之间的万有引力F1、库仑力F2分别满足（　　）

    图1

    A.                    B.

    C.                    D.

    查看答案和解析>>

    如图1所示，两个完全相同的金属球壳a与b，其壳层的厚度和质量分布均匀.将它们固定于绝缘支座上，两球心间的距离l为球半径的三倍.若使它们带上等量异种电荷，使其电荷量的绝对值均为Q，那么a、b两球之间的万有引力F１和库仑力F２分别为（）

    查看答案和解析>>

    如图1所示，一轻绳跨过一固定的滑轮，两端各连接质量分别为m１和m２的物体.为不失一般性，设m１＜m２.放手后m２将加速下降，m１加速上升，加速度大小均为a.注意此时轻绳也将做变速运动，为判断绳中张力大小是否处处相等，如图1中所示可以隔离质量为Δm的一小段绳子加以研究，其受力分析如图2所示，Δmg为绳子本身所受的重力，F１、F２分别为上、下绳子的拉力.由牛顿第二定律有Δmg＋F２－F１＝Δma.由于整段绳为轻绳即质量可以忽略不计，故Δm趋近于零，而加速度a为有限值，因此F２＝F１，即不论轻绳是否平衡均满足张力大小处处相等.
    力学问题的研究对象中有很多所谓的轻小物体，其特点之一就是可以忽略质量，同时也可以忽略重力.从上面的分析知可同样对其作受力分析，利用牛顿运动定律求解有关问题.
    例2   如图3所示，一小球在纸面内来回摆动.当轻绳OA与OB拉力相等时，摆线OC与竖直面夹角θ为（　　  　）
    A.15°   B.30°   C.45°   D.60°

    查看答案和解析>>


    同步练习册答案