
题目列表(包括答案和解析)
牛顿发现了万有引力定律后,由于不知道引力常量G的数值,因而无法计算出物体之间的引力大小.直到100多年后,英国物理学家卡文迪许通过巧妙的扭秤实验,测定出了引力常量G的数值.实验装置如图所示.他在实验中,采用了“微量放大”的方法,即把万有引力作用下石英丝的扭转角度放大,以便于测量,从而开创了“微力”测量的新方法.物理实验中常有一些新颖的思想和方法使实验取得成功.试根据以前学过的知识,说出两种物理实验思想和方法.

英国物理学家牛顿曾经猜想地面上的重力、地球吸引月球与太阳吸引行星的力遵循同样的“距离平方反比”规律,牛顿为此做了著名的“月一地”检验。牛顿根据检验的结果,把“距离平方反比”规律推广到自然界中任意两个物体间,发现了具有划时代意义的万有引力定律。
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律。设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R) 。那么月球绕地球运行的向心加速度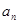 与地面的重力加速度
与地面的重力加速度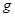 的比值
的比值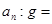 1: 。
1: 。
(2)实测数据验算:月球绕地球运行的轨道半径r=3.80×108m,月 球运行周期T=27.3天=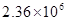 s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度
s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度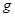 的比值
的比值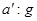 =1: 。
=1: 。
若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律!
英国物理学家牛顿曾经猜想地面上的重力、地球吸引月球与太阳吸引行星的力遵循同样的“距离平方反比”规律,牛顿为此做了著名的“月一地”检验。牛顿根据检验的结果,把“距离平方反比”规律推广到自然界中任意两个物体间,发现了具有划时代意义的万有引力定律。
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律。设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R) 。那么月球绕地球运行的向心加速度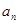 与地面的重力加速度
与地面的重力加速度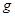 的比值
的比值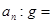 1: 。
1: 。
(2)实测数据验算:月球绕地球运行的轨道半径r=3.80×108m,月
球运行周期T=27.3天=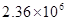 s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度
s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度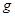 的比值
的比值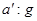 =1: 。
=1: 。
若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律!
 与地面的重力加速度
与地面的重力加速度 的比值
的比值 1: 。
1: 。 s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度
s,地面的重力加速度为g=9.80m/s2,由此计算月球绕地 球运行的向心加速度a´与地面的重力加速度 的比值
的比值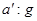 =1: 。
=1: 。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com