
题目列表(包括答案和解析)
|
| 组别 | 摆球材料 | 摆长L/m | 最大摆角 | 全振动次数 N |
| A | 铜 | 0.40 | 15° | 20 |
| B | 铁 | 1.00 | 5° | 50 |
| C | 铝 | 0.40 | 15° | 10 |
| D | 木 | 1.00 | 5° | 50 |
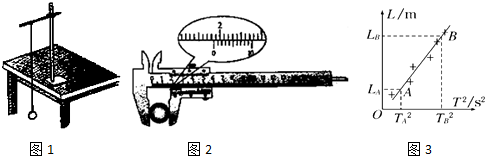
根据单摆周期公式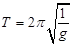 ,可以通过实验测量当地的重力加速度。如图1所示,将细线的上端固定在铁架台上,下端系一小钢球,就做成了单摆。
,可以通过实验测量当地的重力加速度。如图1所示,将细线的上端固定在铁架台上,下端系一小钢球,就做成了单摆。
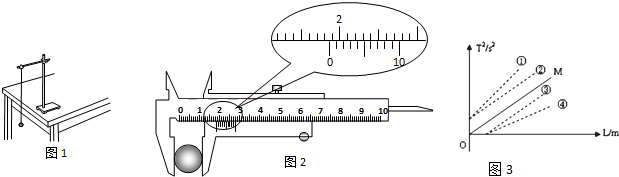
(1).用游标卡尺测量小钢球直径,求数如图2所示,读数为_______mm。
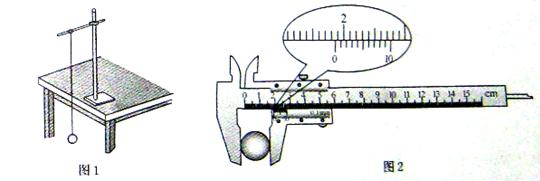
(2).以下是实验过程中的一些做法,其中正确的有______。
a.摆线要选择细些的、伸缩性小些的,并且尽可能长一些
b.摆球尽量选择质量大些、体积小些的
c.为了使摆的周期大一些,以方便测量,开始时拉开摆球,使摆线相距平衡位置有较大的角度
d.拉开摆球,使摆线偏离平衡位置大于50,在释放摆球的同时开始计时,当摆球回到开始位置时停止计时,此时间间隔△t即为单摆周期T
e.拉开摆球,使摆线偏离平衡位置不大于50,释放摆球,当摆球振动稳定后,从平衡位置开始计时,记下摆球做50次全振动所用的时间△t,则单摆周期T=△t /50
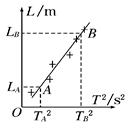
(3).若该实验单摆静止时摆球重心在球心的正下方,仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图所示.采用恰当的数据处理方法也能正确的求出当地的重力加速度,则计算重力加速度的表达式应为g=________.
在“用单摆测重力加速度”的实验中,某同学的主要操作步骤如下:
a.取一根符合实验要求的摆线,下端系一金属小球,上端固定在O点;
b.在小球静止悬挂时测量出O点到小球球心的距离l;
c.拉动小球使细线偏离竖直方向一个不大的角度(约为5°),然后由静止释放小球;
d.用秒表记录小球完成n次全振动所用的时间t。
①用所测物理量的符号表示重力加速度的测量值,其表达式为g= ;
②若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能是 。(选填下列选项前的序号)
A. 测量摆长时,把摆线的长度当成了摆长
B. 摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长
C. 测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期
D. 摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后,为了减小实验误差,他决定用图象法处理数据,并通过改变摆长,测得了多组摆长l和对应的周期T,并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k,则重力加速度的测量值g= 。
④这位同学查阅资料得知,单摆在最大摆角q较大时周期公式可近似表述为![]() 。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。

(10分)在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下:
A.取一根符合实验要求的摆线,下端系一金属小球,上端固定在O点;
B.在小球静止悬挂时测量出O点到小球球心的距离l;
C.拉动小球使细线偏离竖直方向一个不大的角度(约为5°),然后由静止释放小球;
D.用秒表记录小球完成n次全振动所用的时间t。
①用所测物理量的符号表示重力加速度的测量值,其表达式为g= ;
②若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能是
(选填下列选项前的序号)
A、测量摆长时,把摆线的长度当成了摆长
B、摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长
C、测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期
D、摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后,为了减小实验误差,他决定用图象法处理数据,并通过改变摆长,测得了多组摆长l和对应的周期T,并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k,则重力加速度的测量值g= 。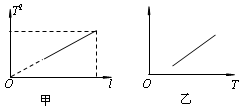
④这位同学查阅资料得知,单摆在最大摆角q较大时周期公式可近似表述为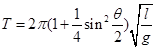 。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com