练习册

  • 练习册
  • 试题
    如图3所示.一根轻质弹簧的一端系着一个物体.手拉轻质弹簧的一端.轻质弹簧与物体一起在光滑水平面上向左做匀加速运动.当手突然停止运动时.物体将( ) A. 立即停止 B. 向左做变加速运动 C. 向左做匀加速运动 D. 向左做减速运动 【查看更多】

     

    题目列表(包括答案和解析)

    如图3所示，

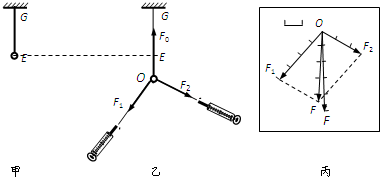
    一根轻质弹簧上端固定在O点，下端拴一个钢球P，球处于静止状态.现对球施加一个方向水平向右的外力F，使球缓慢偏移，在移动的每一个时刻，都可以认为钢球处于平衡状态.若外力F方向始终水平，移动至弹簧与竖直方向的夹角θ=90°且弹簧的伸长量不超过弹性限度，则下面给出的弹簧伸长量x与cosθ的函数关系图象在图4中最接近的是（）

    查看答案和解析>>

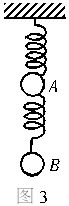
    如图3所示，两根轻弹簧下面均连接一个质量为m的小球，上面一根弹簧的上端固定在天花板上，两小球之间通过一根不可伸长的细线相连接，细线受到的拉力大小等于4mg.当剪断两球之间的细线瞬间，关于球A的加速度大小aA、球B的加速度大小aB以及弹簧对天花板的拉力大小T，以下说法正确的是（）
    A.aA=0、aB=2g、T=2mg
    B.aA=4g、aB=4g、T=2mg
    C.aA=4g、aB=2g、T=4mg
    D.aA=0、aB=4g、T=4mg

    查看答案和解析>>

    取一根轻质弹簧，上端固定在铁架台上，下端系一金属小球，如图所示．把小球沿竖直方向拉离平衡位置后释放，小球将在竖直方向做简谐运动（此装置也称竖直弹簧振子）．将一个电动传感器接到计算机上，就可以测量弹簧快速变化的力，用这种方法测得弹簧对金属小球拉力的大小随时间变化的曲线如图所示，根据此图提供的信息可知：
    （1）摆球的摆动周期T=
    0.6
    0.6
    秒
    （2）t=0.2s时摆球正好经过
    最低点
    最低点
    ．（选填“最低点”、“最高点”或“平衡位置”）

    一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系．他多次换用不同质量的小球并测得相应的周期，现将测得的六组数据，用“?”标示在以m为横坐标、T2为纵坐标的坐标纸上，如上图．
    （3）根据图中给出的数据作出T2与m的关系图线．
    （4）假设图中图线的斜率为b，写出T2与m的关系式为
    T2=bm
    T2=bm
    ．
    （5）求得斜率b的值是
    1.25s2/kg．
    1.25s2/kg．
    ．

    查看答案和解析>>

    如图甲所示，在竖直平面内，将小圆环挂在橡皮条的下端，橡皮条长度为GE．用两根弹簧测力计拉动小圆环到O点，小圆环受到作用力F1、F2和橡皮条的拉力F0，如图乙所示．
    精英家教网
    （1）如图乙，此时要记录下拉力F1、F2的大小，并在白纸上作出
     
    ，以及O点的位置．
    （2）实验中，不必要的是
     
    ．
    A．选用轻质小圆环
    B．弹簧测力计在使用前应校零
    C．撤去F1、F2，改用一个力拉住小圆环，仍使它处于O点
    D．用两根弹簧测力计拉动小圆环时，要保持两弹簧测力计相互垂直
    （3）图丙中F′是用一个弹簧测力计拉小圆环时，在白纸上根据实验结果画出的图示．F与F′中，方向一定沿GO方向的是
     
    ．

    查看答案和解析>>

    取一根轻质弹簧，上端固定在铁架台上，下端系一金属小球，如图甲所示.把小球沿竖直方向拉离平衡位置后释放，小球将在竖直方向做简谐运动（此装置也称竖直弹簧振子）.一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系.他多次换用不同质量的小球并测得相应的周期，现将测得的六组数据，用“·”标示在以m为横坐标、T2为纵坐标的坐标纸上，如图乙所示.

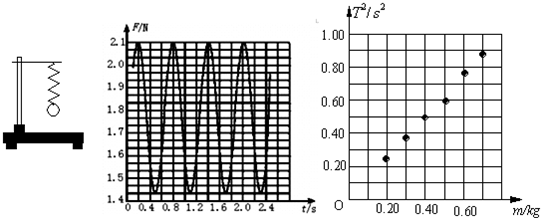
    （1）根据图乙中给出的数据作出T2与m的关系图线；

    （2）假设图乙中图线的斜率为b，写出T与m的关系式；

    （3）求得斜率b的值是多少？（保留两位有效数字）

    查看答案和解析>>


    同步练习册答案