
题目列表(包括答案和解析)
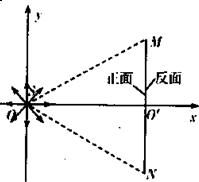 如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O'点.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力.
如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O'点.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力.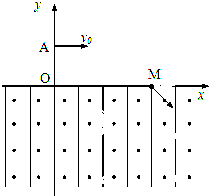 如图所示,直角坐标系位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的方向垂直xOy平面向外,电场线方向平行于y轴.一质量为m.电荷量为q的带正电的小球,从y轴上的A点以水平速度v0向右抛出,与x轴成45°角经x轴上M点进入电场和磁场,恰能做匀速圆周运动,从坐标系原点第一次离开电场和磁场.不计空气阻力,重力加速度为g.求:
如图所示,直角坐标系位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的方向垂直xOy平面向外,电场线方向平行于y轴.一质量为m.电荷量为q的带正电的小球,从y轴上的A点以水平速度v0向右抛出,与x轴成45°角经x轴上M点进入电场和磁场,恰能做匀速圆周运动,从坐标系原点第一次离开电场和磁场.不计空气阻力,重力加速度为g.求:如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O'点。已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力。
(1)若只在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧射出的所有粒子都能打到荧光屏MN上,试求电场强度的最小值Emin及此条件下打到荧光屏M点的粒子的动能;
(2)若在力xOy平面内只加一方向垂直纸面向里的匀强磁场,要使粒子能打到荧光屏MN的反面O'点,试求磁场的磁感应强度的最大值Bmax;
(3)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,磁感应强度与(2)题中所求Bmax相同,试求粒子打在荧光屏MN的正面O'点所需的时间t1和打在荧光屏MN的反面O'点所需的时间t2之比。
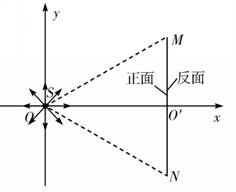
如图所示,在直角坐标系My的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O'点。已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力。
(1) 若只在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧射出的所有粒子都能打到荧光屏MN上,试求电场强度的最小值Emin及此条件下打到荧光屏M点的粒子的动能;
(2) 若在力xOy平面内只加一方向垂直纸面向里的匀强磁场,要使粒子能打到荧光屏MN的反面O'点,试求磁场的磁感应强度的最大值Bmax ;
(3) 若在xOy平面内只加一方向垂直纸面向里的匀强磁场,磁感应强度与(2)题中所求Bmax相同,试求粒子打在荧光屏MN的正面O'点所需的时间t1和打在荧光屏MN的反面O'点所需的时间t2之比。
如图所示,平行板电容器MN竖直放置,极板长为L,两板间的距离也等于L。由离子源产生的带正电粒子的比荷q/m=1.0×1010C/Kg,以v0=1.0×106m/s的速度从板间的某处竖直向上进入平行板,在两板之间加一个适当的偏转电压U,可使粒子恰好从N板的边缘处飞出,且粒子的速度大小变为v=2.0×106m/s,不计粒子的重力,求:[ ]
1.偏转电压U多大?[ ]
2.以N板的边缘为原点,建立图示的坐标系xoy,在y轴右侧有一个圆心位于x轴、半径r=0.01m的圆形磁场区域,磁感应强度B=0.01T,方向垂直纸面向外,有一垂直于x轴的面积足够大的竖直荧光屏PQ置于某处。若圆形磁场可沿x轴移动,圆心O’在x轴上的移动范围为[0.01m,+∞],发现粒子打在荧光屏上方最远点的位置为y=2cm,求粒子打在荧光屏下方最远点的位置坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com