如图甲为两种光以相同的入射角从某种介质射向真空时的光路图．图乙为杨氏双缝干涉实验示意图，其中S₁、S₂为双缝，D为光屏，实验中观察到屏上O点为中央亮纹的中心．下列说法正确的是（      ）

A．由图甲可知，a光的全反射临界角小于b光的全反射临界角

B．通过图乙中的双缝干涉装置，a光的干涉条纹间距比b光的宽

C．在其它条件不变的情况下，若将D屏向右平移一段距离，则屏上干涉条纹间距将变大

D．由实验观察知P₁为a光的第一级亮纹的中心，在其它条件不变的情况下，若将D屏向右平移一段距离，屏上P₁位置仍然为a光的亮纹的中心

（8分）【物理—物理3-4】

（1）某波源 P 的振动图像如图所示，已知该波在某种介质中传播速度为 v = 2 m/s，从图中计时时刻开始，画出 t = 0．3s 时刻，该波源向外传播的波形图（至少一个波长），并在图中标注出 P 点位置．

（2）如图甲所示，在杨氏双缝干涉实验中，光屏中央 O 点应该是出现的是

                     （选填“明条纹”或“暗条纹”）．现将两狭缝 S₁、S ₂  之间的距离变小，仍用上述光源进行上述实验，保持其他条件不变，则屏上的条纹间距将

                         （选填“变宽”、“变窄”或“不变”）．

（3）如图所示，一束激光从O 点由空气射入厚度均匀的介质，经下表面反射后，从上面的 A 点射出；已知入射角为 θ ₁ ，A 与 O 相距 l ，介质的折射率为  n ，光在空气中的传播速度为 c ．试求光在介质中的传播时间 t ．

（25分）图1所示为杨氏双缝干涉实验的示意图，取纸面为yz平面。y、z轴的方向如图所示。线光源S通过z轴，双缝S₁、S₂对称分布在z轴两侧，它们以及屏P都垂直于纸面。双缝间的距离为d，光源S到双缝的距离为l，双缝到屏的距离为D，，。

　　1.从z轴上的线光源S出发经S₁、S₂不同路径到P0点的光程差为零，相干的结果产生一亮纹，称为零级亮纹。为了研究有一定宽度的扩展光源对于干涉条纹清晰度的影响，我们先研究位于轴外的线光源S′形成的另一套干涉条纹，S′位于垂直于z轴的方向上且与S平行，两者相距，则由线光源S′出发分别经S₁、S₂产生的零级亮纹，与P₀的距离

　　2.当光源宽度为的扩展光源时，可将扩展光源看作由一系列连续的、彼此独立的、非相干的线光源组成。这样，各线光源对应的干涉条纹将彼此错开，在屏上看到的将是这些干涉条纹的光强相加的结果，干涉条纹图像将趋于模糊，条纹的清晰度下降。假设扩展光源各处发出的光强相同、波长皆为。当增大导致零级亮纹的亮暗将完全不可分辨，则此时光源的宽度

　　3.在天文观测中，可用上述干涉原理来测量星体的微小角直径。遥远星体上每一点发出的光到达地球处都可视为平行光，从星体相对的两边缘点发来的两组平行光之间的夹角就是星体的角直径。遥远星体的角直径很小，为测量如些微小的角直径，迈克尔逊设计了测量干涉仪，其装置简化为图2所示。M1、M2、M3、M4是四个平面反射镜，它们两两平行，对称放置，与入射光（a、 a′）方向成45°角。S1和S2是一对小孔，它们之间的距离是d。M1和M2可以同步对称调节来改变其中心间的距离h。双孔屏到观察屏之间的距离是D。a、 a′和b、 b′分别是从星体上相对着的两边缘点发来的平行光束。设光线a、 a′垂直双孔屏和像屏，星光的波长是，试导出星体上角直径的计算式。

注：将星体作圆形扩展光源处理时，研究扩展光源的线度对于干涉条纹图像清晰度的影响会遇到数学困难，为简化讨论，本题拟将扩展光源作宽度为的矩形光源处理。

（25分）图1所示为杨氏双缝干涉实验的示意图，取纸面为yz平面。y、z轴的方向如图所示。线光源S通过z轴，双缝S₁、S₂对称分布在z轴两侧，它们以及屏P都垂直于纸面。双缝间的距离为d，光源S到双缝的距离为l，双缝到屏的距离为D，，。

　　1.从z轴上的线光源S出发经S₁、S₂不同路径到P0点的光程差为零，相干的结果产生一亮纹，称为零级亮纹。为了研究有一定宽度的扩展光源对于干涉条纹清晰度的影响，我们先研究位于轴外的线光源S′形成的另一套干涉条纹，S′位于垂直于z轴的方向上且与S平行，两者相距，则由线光源S′出发分别经S₁、S₂产生的零级亮纹，与P₀的距离

　　2.当光源宽度为的扩展光源时，可将扩展光源看作由一系列连续的、彼此独立的、非相干的线光源组成。这样，各线光源对应的干涉条纹将彼此错开，在屏上看到的将是这些干涉条纹的光强相加的结果，干涉条纹图像将趋于模糊，条纹的清晰度下降。假设扩展光源各处发出的光强相同、波长皆为。当增大导致零级亮纹的亮暗将完全不可分辨，则此时光源的宽度

　　3.在天文观测中，可用上述干涉原理来测量星体的微小角直径。遥远星体上每一点发出的光到达地球处都可视为平行光，从星体相对的两边缘点发来的两组平行光之间的夹角就是星体的角直径。遥远星体的角直径很小，为测量如些微小的角直径，迈克尔逊设计了测量干涉仪，其装置简化为图2所示。M1、M2、M3、M4是四个平面反射镜，它们两两平行，对称放置，与入射光（a、 a′）方向成45°角。S1和S2是一对小孔，它们之间的距离是d。M1和M2可以同步对称调节来改变其中心间的距离h。双孔屏到观察屏之间的距离是D。a、 a′和b、 b′分别是从星体上相对着的两边缘点发来的平行光束。设光线a、 a′垂直双孔屏和像屏，星光的波长是，试导出星体上角直径的计算式。

注：将星体作圆形扩展光源处理时，研究扩展光源的线度对于干涉条纹图像清晰度的影响会遇到数学困难，为简化讨论，本题拟将扩展光源作宽度为的矩形光源处理。

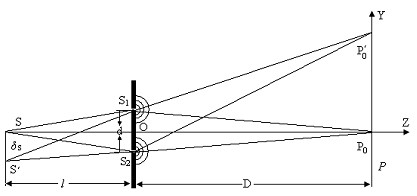
图1

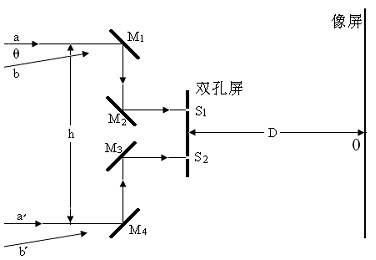
图2