如图甲所示为汤姆生在1897年测量阴极射线（电子）的比荷时所用实验装置的示意图．K为阴极，A₁和A₂为连接在一起的中心空透的阳极，电子从阴极发出后被电场加速，只有运动方向与A₁和A₂的狭缝方向相同的电子才能通过，电子被加速后沿00’方向垂直进人方向互相垂直的电场、磁场的叠加区域．磁场方向垂直纸面向里，电场极板水平放置，电子在电场力和磁场力的共同作用下发生偏转．已知圆形磁场的半径为r，圆心为C．
某校物理实验小组的同学们利用该装置，进行了以下探究测量：
第一步：调节两种场的强弱．当电场强度的大小为E，磁感应强度的大小为B时，使得电子恰好能够在复合场区域内沿直线运动．
第二步：撤去电场，保持磁场和电子的速度不变，使电子只在磁场力的作用下发生偏转，打在荧屏上出现一个亮点P，通过推算得到电子的偏转角为α（CP与OO′下之间的夹角）．
求：（1）电子在复合场中沿直线向右飞行的速度；
（2）电子的比荷

e

m

；
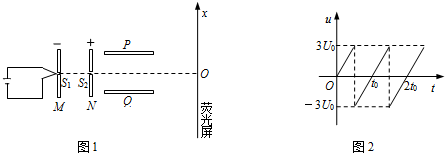
（3）有位同学提出了该装置的改造方案，把球形荧屏改成平面荧屏，并画出了如图乙的示意图．已知电场平行金属板长度为L₁，金属板右则到荧屏垂直距离为L₂．实验方案的第一步不变，可求出电子在复合场中沿直线向右飞行的速度．第二步撤去磁场，保持电场和电子的速度不变，使电子只在电场力的作用下发生偏转，打在荧屏上出现一个亮点P，通过屏上刻度可直接读出电子偏离屏中心点的距离

.

O/Q

=y．同样可求出电子的比荷

e

m

．请你判断这一方案是否可行？并说明相应的理由．

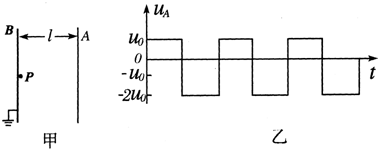如图甲所示，A、B是真空中的两块面积很大的平行金属板，相距为L，加上周期为了的交流电压，在两板间产生交变的匀强电场．已知B板的电势为零，A板的电势U_A随时间变化的规律如图乙所示，其中U_A最大值为U₀，最小值为-2U₀．在靠近B板的P点处，不断地产生电量为q、质量为m的带负电的微粒，各个时刻产生带电微粒的机会均等，这种微粒产生后，从静止出发在电场力的作用下运动，设微粒一旦碰到金属板，它就附在板上不再运动，且其电量同时消失，不影响A、B板的电压．已知上述的T、U₀、L、g和m等各量正好满足等式L²=3U₀q（T/2）²/16m，若在交流电压变化的每个周期T内，平均产生400个上述微粒．求（不计重力，不考虑微粒之间的相互作用）：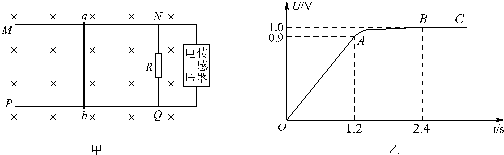
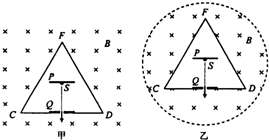（1）从t=0开始运动的微粒到达A板所用的时间．
（2）在t=0到t_c=T/2这段时间内产生的微粒中，有多少个微粒可到达A板．

如图甲所示，MN、PQ是固定于同一水平面内相互平行的粗糙长直导轨，间距L=2.0m，R是连在导轨一端的电阻，质量m=1.0kg的导体棒ab垂直跨在导轨上，电压传感器与这部分装置相连．导轨所在空间有磁感应强度B=0.50T、方向竖直向下的匀强磁场．从t=0开始对导体棒ab施加一个水平向左的拉力，使其由静止开始沿导轨向左运动，电压传感器测出R两端的电压随时间变化的图线如图乙所示，其中OA、BC段是直线，AB段是曲线．假设在1.2s以后拉力的功率P=4.5W保持不变．导轨和导体棒ab的电阻均可忽略不计，导体棒ab在运动过程中始终与导轨垂直，且接触良好．不计电压传感器对电路的影响．g取10m/s²．求：
（1）导体棒ab最大速度v_m的大小；
（2）在1.2s～2.4s的时间内，该装置总共产生的热量Q；
（3）导体棒ab与导轨间的动摩擦因数μ和电阻R的值．

如图1所示，电子显像管由电子枪、加速电场、偏转场及荧光屏组成．M、N为加速电板，加速电压为U₀，S₁、S₂为板上正对的小孔．金属板P和Q水平放置，两板的长度和两板间的距离均为l；距右边缘l处有一荧光屏，取屏上与S₁、S₂共线的O点为原点，向上为正方向建立x轴．电子枪发射质量为m，电荷量为-e的电子，初速度可以忽略，电子经加速电场后从小孔S₂射入偏转场．不计电子重力和电子之间的相互作用．
（1）求电子到达小孔S₂时的速度大小v；
（2）若板P、Q间只存在垂直于纸面向外的匀强磁场，电子刚好经过P板的右边缘后，打在荧光屏上．求磁感应强度大小B和电子打在荧光屏上的位置坐标x；
（3）若板P和Q间只存在电场，板间电压u随时间t的变化关系如图2所示，单位时间内从小孔S₁进入的电子个数为N．电子打在荧光屏上形成一条亮线．若在一个周期内单位长度亮线上的电子个数相同，求2t₀时间内打到单位长度亮线上的电子个数n（忽略电场变化产生的磁场；可以认为每个电子在板P和Q间运动过程中，两板间的电压恒定）．

如图甲所示，在空心三棱柱CDF以外足够大的空间中，充满着磁感应强度为B的匀强磁场．三棱柱的轴线与磁场平行，截面边长为L，三棱柱用绝缘薄板材料制成，其内部有平行于CD侧面的金属板P、Q，两金属板间的距离为d，P板带正电，Q板带负电，Q板中心有一小孔，P板上与小孔正对的位置有一个粒子源S，从S处可以发出初速度为0、带电量为+q、质量为m的粒子，这些粒子与三棱柱侧面碰撞时无能量损失．试求：
（1）为使从S点发出的粒子最终又回到S点，P、Q之间的电压U应满足什么条件？（Q与CD之间距离不计）
（2）粒子从S点出发又回到S点的最短时间是多少？
（3）若磁场是半径为a的圆柱形区域，如图乙所示，圆柱的轴线与三棱柱的轴线重合，且a=（

3

3

+

1

10

）L，要使S点发出的粒子最终又回到S点，则P、Q之间的电压不能超过多少？