
题目列表(包括答案和解析)
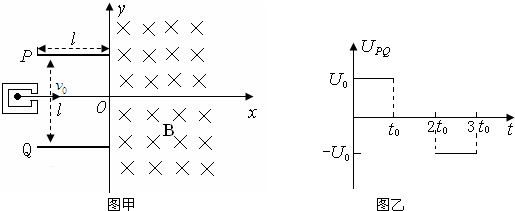 如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里.位于极板左侧的粒子源沿x轴向右连续发射质量为m、电量为+q、速度相同、重力不计的带电粒子.在两板间加上如图乙所示的周期性变化的电压(不考虑极板边缘的影响).已知t=0时刻进入两板间的带电粒子恰好在2t0时刻经极板边缘射入磁场.上述m、q、l、t0、B为已知量.(不考虑粒子间相互影响及返回板间的情况)(若tanθ=b,θ∈(-
如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里.位于极板左侧的粒子源沿x轴向右连续发射质量为m、电量为+q、速度相同、重力不计的带电粒子.在两板间加上如图乙所示的周期性变化的电压(不考虑极板边缘的影响).已知t=0时刻进入两板间的带电粒子恰好在2t0时刻经极板边缘射入磁场.上述m、q、l、t0、B为已知量.(不考虑粒子间相互影响及返回板间的情况)(若tanθ=b,θ∈(-| π |
| 2 |
| π |
| 2 |

| A、带电粒子飞入匀强磁场后,一定做匀速圆周运动 | B、带电粒子飞入匀强磁场后做匀速圆周运动时,速度一定不变 | C、带电粒子飞入匀强磁场后做匀速圆周运动时,洛仑兹力方向与运动方向平行 | D、带电粒子飞入匀强磁场后做匀速圆周运动时,动能一定保持不变 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com