
题目列表(包括答案和解析)
 两同学分别用不同的方法测定一半圆柱形玻璃砖的折射率.
两同学分别用不同的方法测定一半圆柱形玻璃砖的折射率.| sinθ2 |
| sinθ1 |
| sinθ2 |
| sinθ1 |
| R |
| L |
| R |
| L |
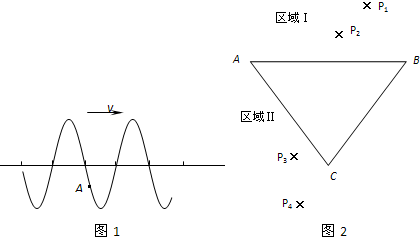 (2010?烟台一模)(1)如图1是一列向右传播的横波在t时刻的波形图,波的周期为T,请在图中画出:
(2010?烟台一模)(1)如图1是一列向右传播的横波在t时刻的波形图,波的周期为T,请在图中画出:| 1 | 4 |
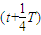 时刻的波形图.
时刻的波形图.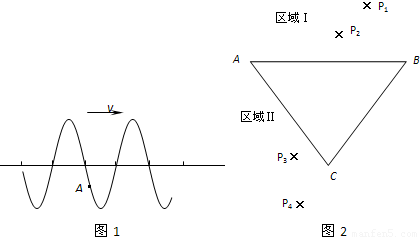
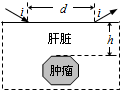 “B超”可用于探测人体内脏的病变状况.如图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为
“B超”可用于探测人体内脏的病变状况.如图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为| sinθ1 |
| sinθ2 |
| v1 |
| v2 |

A.增大入射角i,光束会在aa′介面发生全反射
B.增大入射角i,光束会在bb′介面发生全反射
C.无论i如何变化,这束光都不可能发生全反射
D.光束从bb′介面射入空气时,折射角小于i
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com