如图12所示，在周期性变化的匀强磁场区域内有垂直于磁场的一个半径r=1 m、电阻为R=3.14 Ω的金属圆形线框，当磁场按图乙所示规律变化时，线框中有感应电流产生.

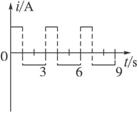
图12

(1)在丙图中画出感应电流随时间变化的i-t图象（以逆时针方向为正）.

(2)求出线框中感应电流的有效值.

16.如图12所示，在一个圆形域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A₂A₄为边界的两个半圆形区域Ⅰ、Ⅱ中，A₂A₄与A₁A₃的夹角为60°.一质量为m、带电量为 +q 的粒子以某一速度从Ⅰ区的边缘点A₁处沿与A₁A₃成30°角的方向射入磁场，随后该粒子以垂直于A₂A₄的方向经过圆心O进入Ⅱ区，最后再从A₄处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小（忽略粒子重力）。

如图12所示，足够长的两光滑导轨水平放置，两条导轨相距为d，左端MN用阻值不计的导线相连，金属棒ab可在导轨上滑动，导轨单位长度的电阻为r₀，金属棒ab的电阻不计.整个装置处于竖直向下的均匀磁场中，磁场的磁感应强度随时间均匀增加，B=kt，其中k为常数.金属棒ab在水平外力的作用下，以速度v沿导轨向右做匀速运动，t=0时，金属棒ab与MN相距非常近.求：

图12

（1）当t=t₀时，水平外力的大小F；

（2）同学们在求t=t₀时刻闭合回路消耗的功率时，有两种不同的求法：

方法一：P=F·v

方法二：BId=F  I=  P=I²R=（其中R为回路总电阻）

这两种方法哪一种正确？请你做出判断，并简述理由.

如图12所示，一个被x轴与曲线方程（m）所围的空间中存在着匀强磁场。磁场方向垂直纸面向里，磁感应强度B=0.2T。正方形金属线框的边长是L=0.40m，电阻是R=0.1Ω，它的一边与x轴重合，在拉力F的作用下，线框以v=10m/s的速度水平向右匀速运动。试求：

（1）拉力F的最大功率是多少？

（2）拉力F要做多少功才能把线框拉过磁场区？

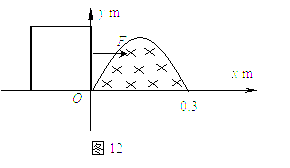
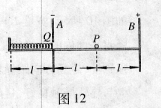
       如图12所示，A、B是两块竖直放置的平行金属板，相距为，分别带有等量的负、正电荷，在两板间形成电场强度大小为E的匀强电场。A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道，一个质量为，电荷量为的小球（可视为质点）， 在外力作用下静止在轨道的中点P处。孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板处有一固定档板，长为的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q。撤去外力释放带电小粒，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能。小球从接触 Q开始，经历时间T₀第一次把弹簧压缩至最短，然后又被弹簧弹回。由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的。求：

（1）小球第一次接触Q时的速度大小；

（2）假设小球第次弹回两板间后向右运动的最远处没有到达B板，试导出小球从第次接触 Q，到本次向右运动至最远处的时间T₀的表达式；

（3）假设小球被第N次弹回两板间后向右运动最远处恰好到达B板，求N为多少。