
题目列表(包括答案和解析)
 如图所示,截面积为S的气缸A用一个带有阀门K的细管与容器B连通(细管的容积不计).开始时K关闭,气缸A内充有一定质量的理想气体,B内为真空,气缸A的活塞上放有砝码,此时A内气体温度为T1,活塞静止时与气缸底部的距离为H.打开阀门K后,活塞下降,若将A、B内气体的温度都升高到T2时,活塞仍可升到原来高度H.已知大气压强为 P0,活塞与气缸壁之间摩擦可忽略不计,试求:
如图所示,截面积为S的气缸A用一个带有阀门K的细管与容器B连通(细管的容积不计).开始时K关闭,气缸A内充有一定质量的理想气体,B内为真空,气缸A的活塞上放有砝码,此时A内气体温度为T1,活塞静止时与气缸底部的距离为H.打开阀门K后,活塞下降,若将A、B内气体的温度都升高到T2时,活塞仍可升到原来高度H.已知大气压强为 P0,活塞与气缸壁之间摩擦可忽略不计,试求: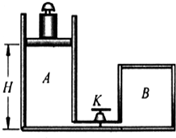

 一横截面积为S的气缸水平放置、固定不动、气缸壁是导热的.两个活塞A和B将气缸分隔为1、2两个气室,达到平衡时1、2两个气室体积比为3:2.如图所示.在室温不变的条件下,缓慢推动活塞A,使之向右移动一段距离d.求活塞B向右移动的距离.(不计活塞与气缸壁之间的摩擦)
一横截面积为S的气缸水平放置、固定不动、气缸壁是导热的.两个活塞A和B将气缸分隔为1、2两个气室,达到平衡时1、2两个气室体积比为3:2.如图所示.在室温不变的条件下,缓慢推动活塞A,使之向右移动一段距离d.求活塞B向右移动的距离.(不计活塞与气缸壁之间的摩擦) | △V |
| △V2 |
| Sd |
| Sx |
| 5 |
| 2 |
| 2 |
| 5 |
 在室温不变的条件下,缓慢推动活塞A,使之向右移动一段距离d.求活塞B向右移动的距离. 不计活塞与气缸壁之间的摩擦.
在室温不变的条件下,缓慢推动活塞A,使之向右移动一段距离d.求活塞B向右移动的距离. 不计活塞与气缸壁之间的摩擦.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com