某物体质量为50kg，将它放置在卫星中的台秤上，当卫星以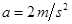的加速度随火箭向上加速升空的过程中，某时刻发现台秤的示数为350N，此时卫星距离地球表面有多远？已知地球半经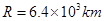，地球表面的重力加速度。（计算结果保留三位有效数字）

某物体质量为50kg，将它放置在卫星中的台秤上，当卫星以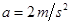的加速度随火箭向上加速升空的过程中，某时刻发现台秤的示数为350N，此时卫星距离地球表面有多远？已知地球半经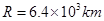，地球表面的重力加速度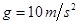。（计算结果保留三位有效数字）

（12分）2005年10月，我国“神舟六号”飞船绕地沿椭圆轨道运行5圈后变轨进入到距地面400公里的圆形轨道上，绕地球飞行约76圈后，顺利进入预定返回轨道．在内蒙接近地面时，返回舱点火，最后成功地实现软着陆（着地时速度为零）．通过以上描述，利用你所学的知识解答以下问题（已知地球半径取6000km，地球表面重力加速度g=10m/s²，计算时取3）

（1）在返回舱离内蒙地面1．5m时，返回舱下落速度达15m/s，为实现软着陆，此时启动5个反推力小火箭，若返回舱重8t，则每支火箭的平均推力约为多大？

　 （2）古代神话中有“天上一天，地上一年”之说．请问飞船在圆形轨道上运动时，地球上一昼夜，费俊龙和聂海胜他们感觉过了几昼夜（第2问保留到整数）?