
题目列表(包括答案和解析)
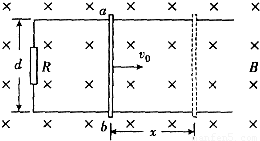
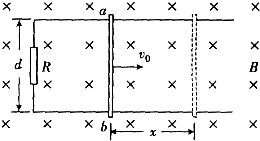 如图所示,在同一水平面内固定有两平行金属导轨,导轨光滑且足够长,间距为d,其左端接阻值为R的定值电阻,整个装置处在竖直向下、磁感应强度为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置.现给杆一水平向右的初速度,经过时间t,导体杆ab向右运动了x,在运动过程中,导体杆ab始终与导轨垂直且接触良好,不计导轨和导体杆ab的电阻.甲、乙两位同学根据以上条件,分别求解在时间t内电阻R放出的热量Q和通过电阻R的电荷量q,具体过程如下:
如图所示,在同一水平面内固定有两平行金属导轨,导轨光滑且足够长,间距为d,其左端接阻值为R的定值电阻,整个装置处在竖直向下、磁感应强度为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置.现给杆一水平向右的初速度,经过时间t,导体杆ab向右运动了x,在运动过程中,导体杆ab始终与导轨垂直且接触良好,不计导轨和导体杆ab的电阻.甲、乙两位同学根据以上条件,分别求解在时间t内电阻R放出的热量Q和通过电阻R的电荷量q,具体过程如下:. |
| E |
| △Φ |
| t |
| Bdx |
| t |
. |
| I |
| ||
| R |
| Bdx |
| tR |
. |
| F |
. |
| I |
| B2d2x |
| tR |
. |
| F |
| B2d2x2 |
| tR |
. |
| E |
| △Φ |
| t |
| Bdx |
| t |
. |
| I |
| ||
| R |
| Bdx |
| tR |
. |
| I |
| Bdx |
| R |

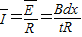
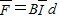 =
=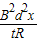
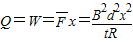
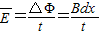
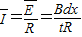
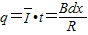
如图所示,在同一介质的一条直线上两个振源A、B相距6m,振动频率相等,从t0=0时刻A、B开始振动,且都只振动一个周期,振幅相等,甲为A点的振动图像,乙为B点的振动图像。若A向右传播的波与B向左传播的波在t1 = 0.3s时相遇,则
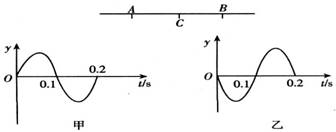
A.两列波在A、B间的传播速度均为10m/s
B.两列波的波长都是4m
C.在两列波相遇过程中,中点C为振动加强点
D.t2 = 0.7s时刻B点经过平衡位置且振动方向向下
如图(甲)所示为一种研究高能粒子相互作用的装置,两个直线加速器均由k个长度逐个增长的金属圆筒组成(整个装置处于真空中。图中只画出了6个圆筒,作为示意),它们沿中心轴线排列成一串,各个圆筒相间地连接到频率为f、最大电压值为U的正弦交流电源的两端。设金属圆筒内部没有电场,且每个圆筒间的缝隙宽度很小,带电粒子穿过缝隙的时间可忽略不计。为达到最佳加速效果,应当调节至粒子穿过每个圆筒的时间恰为交流电的半个周期,粒子每次通过圆筒间缝隙时,都恰为交流电压的峰值。
质量为m、电荷量为e的正、负电子分别经过直线加速器加速后,从左、右两侧被导入装置送入位于水平面内的圆环形真空管道,且被导入的速度方向与圆环形管道中粗虚线相切。在管道内控制电子转弯的是一系列圆形电磁铁,即图中的A1、A2、A3……An,共n个,均匀分布在整个圆周上(图中只示意性地用细实线和细虚线了几个),每个电磁铁内的磁场都是磁感应强度和方向均相同的匀强磁场,磁场区域都是直径为d的圆形。改变电磁铁内电流的大小,就可改变磁场的磁感应强度,从而改变电子偏转的角度。经过精确的调整,可使电子在环形管道中沿图中粗虚线所示的轨迹运动,这时电子经过每个电磁铁时射入点和射出点都在电磁铁的一条直径的两端,如图(乙)所示。这就为实现正、负电子的对撞作好了准备。
(1)若正电子进入第一个圆筒的开口时的速度为v0,且此时第一、二两个圆筒的电势差为U,正电子进入第二个圆筒时的速率多大?
(2)正、负电子对撞时的速度多大?
(3)为使正电子进入圆形磁场时获得最大动能,各个圆筒的长度应满足什么条件?
(4)正电子通过一个圆形磁场所用的时间是多少?


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com