
题目列表(包括答案和解析)
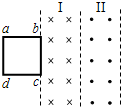 空间内有两个沿竖直方向的有界匀强磁场I、II,磁感应强度大小均为B,宽度均为L,边界线平行,磁场I竖直向下,磁场II竖直向上,如图所示为俯视图.一边长为L、质量为m的正方形导线框abcd放在光滑绝缘的水平面上,在水平恒力F作用下沿水平面通过两个磁场区域.线框的bc边始终平行于磁场区的边界,力F垂直于bc边,当bc边进入磁场I时,线框恰以速度v0做匀速运动,此时线框中的电流为i0;当ad边将要离开磁场II时线框中的电流稍小于i0,则( )
空间内有两个沿竖直方向的有界匀强磁场I、II,磁感应强度大小均为B,宽度均为L,边界线平行,磁场I竖直向下,磁场II竖直向上,如图所示为俯视图.一边长为L、质量为m的正方形导线框abcd放在光滑绝缘的水平面上,在水平恒力F作用下沿水平面通过两个磁场区域.线框的bc边始终平行于磁场区的边界,力F垂直于bc边,当bc边进入磁场I时,线框恰以速度v0做匀速运动,此时线框中的电流为i0;当ad边将要离开磁场II时线框中的电流稍小于i0,则( )(20分)如图所示,相互平行的足够长的光滑绝缘轨道MN和PQ水平固定,有一质量为m、电阻为R的水平导体框abcd(其长度ab=cd=L1宽度ad=bc=L2)可沿轨道滑动,滑动时ab、cd边始终保持与轨道垂直。轨道所在空间存在竖直方向的磁场,其磁感应强度B的大小沿x坐标正向(水平向右)按B=kx(k为已知的常数)随坐标x成正比增强。现对导体框施加一大小恒为F的外力,使它由静止开始从坐标原点O开始向右运动,问:
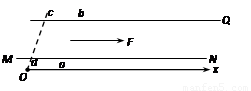
⑴若从上往下看,框中的感应电流方向为顺时针方向,那么磁场方向如何?导体框的运动情况如何?试定性作出描述。
⑵当导体框向右运动的速度为v时,框中的电流为多大?
⑶导体框向右运动能提供的最大电功率为多大?
| A.bc边在磁场II中运动时线框中的电流方向为adcba | ||
B.bc边恰进入磁场II时线框的加速度大小为
| ||
C.bc边恰离开磁场II时线框的速度大小可能为
| ||
| D.bc边在磁场II中运动的过程中线框中电流的最小值一定小于i0 |
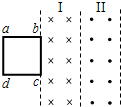


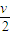
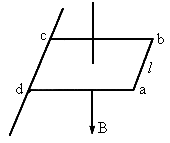
如图所示,匀强磁场的磁感应强度为B,方向竖直向下,在磁场中有一边长为l的正方形导线框,ab边质量为m,其余边质量不计,cd边有固定的水平轴,导线框可以绕其转动,现将导线框拉至水平位置由静止释放,不计摩擦和空气阻力,金属框经过时间t运动到竖直位置,此时ab边的速度为v,求:
(1)此过程中线框产生的平均感应电动势的大小;
(2)线框运动到竖直位置时线框感应电动势的大小;
(3)此过程中线框产生的热量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com