
题目列表(包括答案和解析)
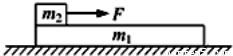
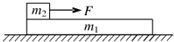 如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( )
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( )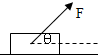 如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )
如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是()
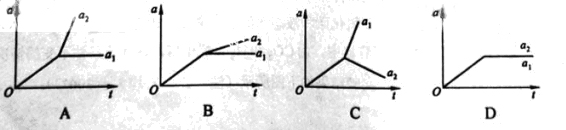
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是( )
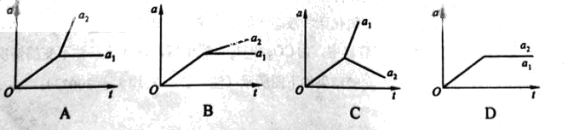
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com