练习册

  • 练习册
  • 试题
    3．如图所示.质量M=4kg的滑板B静止放在光滑水平面上.其右端固定一根轻质弹簧.弹簧的自由端C到滑板左端的距离L=0.5m.这段滑板与木块A之间的动摩擦因数μ＝0.2.而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑．可视为质点的小木块A以速度v0＝10m/s.由滑板B左端开始沿滑板B表面向右运动．已知A的质量m=1kg.g取10m/s2 ．求: (1)弹簧被压缩到最短时木块A的速度, (2)木块A压缩弹簧过程中弹簧的最大弹性势能． [答案]39J 解析:(1)弹簧被压缩到最短时.木块A与滑板B具有相同的速度.设为V.从木块A开始沿滑板B表面向右运动至弹簧被压缩到最短的过程中.A.B系统的动量守恒.则mv0＝(M+m)V ① V=v0 ② 木块A的速度:V＝2m/s ③ (2)木块A压缩弹簧过程中.弹簧被压缩到最短时.弹簧的弹性势能最大． 由能量守恒.得 EP＝ ④ 解得EP＝39J 高三物理上学期十月份每日一题试题 已知A.B两物块的质量分别为m和3m.用一轻质弹簧连接.放在光滑水平面上.使B物块紧挨在墙壁上.现用力推物块A压缩弹簧．这个过程中外力F做功为W.待系统静止后.突然撤去外力．在求弹簧第一次恢复原长时A.B的速度各为多大时.有同学求解如下: 解:设弹簧第一次恢复原长时A.B的速度大小分别为vA.vB 系统动量守恒:0=mvA+3mvB 系统机械能守恒:W= 解得:,(“- 表示B的速度方向与A的速度方向相反) (1)你认为该同学的求解是否正确．如果正确.请说明理由,如果不正确.也请说明理由并给出正确解答． (2)当A.B间的距离最大时.系统的弹性势能EP=? [答案](1)不正确．.vB=0,(2) 解析:(1)该同学的求解不正确．在弹簧恢复原长时.系统始终受到墙壁给它的外力作用.所以系统动量不守恒.且B物块始终不动.但由于该外力对系统不做功.所以机械能守恒.即在恢复原长的过程中.弹性势能全部转化为A物块的动能． 解得.vB=0 (2)在弹簧恢复原长后.B开始离开墙壁.A做减速运动.B做加速运动.当A.B速度相等时.A.B间的距离最大.设此时速度为v.在这个过程中.由动量守恒定律得 mvA=(m+3m)v 解得 根据机械能守恒.有W= 解得 高三物理上学期十月份每日一题试题 如图所示.两个质量均为4m的小球A和B由轻弹簧连接.置于光滑水平面上．一颗质量为m子弹.以水平速度v0射入A球.并在极短时间内嵌在其中．求:在运动过程中 (1)什么时候弹簧的弹性势能最大.最大值是多少? (2)A球的最小速度和B球的最大速度． [答案](1),(2)VAmin.VBmax 解析:子弹与A球发生完全非弹性碰撞.子弹质量为m.A球.B球分别都为M.子弹与A球组成的系统动量守恒.则 mv0= (m+M)V ① (1)以子弹.A球.B球作为一系统.以子弹和A球有共同速度为初态.子弹.A球.B球速度相同时为末态.则 (m+M)V= (m+M+M)V′ ② ③ M＝4m.解得 ④ (2)以子弹和A球有共同速度为初态.子弹和A球速度最小.B球速度最大为末态.则(m+M)V= (m+M)VA+MVB ⑤ ⑥ 解得. ⑦ 或＝v0.＝0 ⑧ 根据题意求A球的最小速度和B球的最大速度.所以VAmin.VBmax 高三物理上学期十月份每日一题试题 如图所示.在足够长的光滑水平轨道上静止三个小木块A.B.C.质量分别为mA=1kg.mB=1kg.mC=2kg.其中B与C用一个轻弹簧固定连接.开始时整个装置处于静止状态,A和B之间有少许塑胶炸药.A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失)．现在引爆塑胶炸药.若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能.A和B分开后.A恰好在B.C之间的弹簧第一次恢复到原长时追上B.并且与B发生碰撞后粘在一起．求: (1)在A追上B之前弹簧弹性势能的最大值, (2)A与B相碰以后弹簧弹性势能的最大值． [答案]0.5J 解析:(1)塑胶炸药爆炸瞬间取A和B为研究对象.假设爆炸后瞬间A.B的速度大小分别为vA.vB.取向右为正方向 由动量守恒:-mAvA+mBvB=0 爆炸产生的热量由9J转化为A.B的动能 代入数据解得vA =vB =3m/s 由于A在炸药爆炸后再次追上B的时候弹簧恰好第一次恢复到原长.则在A追上B之前弹簧已经有一次被压缩到最短.爆炸后取B.C和弹簧为研究系统.当弹簧第一次被压缩到最短时B.C达到共速vBC.此时弹簧的弹性势能最大.设为Ep1． 由动量守恒.得mBvB=(mB+mC)vBC 由机械能守恒.得 代入数据得EP1=3J (2)设B.C之间的弹簧第一次恢复到原长时B.C的速度大小分别为vB1和vC1.则由动量守恒和能量守恒: mBvB=mBvB1+mCvC1 代入数据解得:vB1=-1m/s.vC1=2m/s (vB1 =3m/s.vC1=0m/s不合题意.舍去．) A爆炸后先向左匀速运动.与弹性挡板碰撞以后速度大小不变.反向弹回．当A追上B.发生碰撞瞬间达到共速vAB 由动量守恒.得mAvA+mBvB1=(mA+mB)vAB 解得vAB =1m/s 当A.B.C三者达到共同速度vABC时.弹簧的弹性势能最大为EP2 由动量守恒.得(mA+mB)vAB+mCvC1=(mA+mB+mC)vABC 由能量守恒.得 代入数据得EP2 =0.5J 高三物理上学期十月份每日一题试题 如图所示.滑块A.B的质量分别为m与M.且m＜M.由轻质弹簧相连接.置于光滑的水平面上.用一根轻绳把两滑块拉至最近.使弹簧处于最大压缩状态后绑紧.两滑块一起以恒定的速度v0向右滑动.突然.轻绳断开.当弹簧恢复至自然长度时.滑块A的速度正好为零.问在以后的运动过程中.滑块B是否会有速度为零的时刻?试通过定量分析.证明你的结论． [答案]不可能出现滑块B的速度为零的情况 解析:当滑块A的速度为零时.系统的机械能等于滑块B的动能.设此时滑块B的速度为v.则 ① 由动量守恒定律.得 ② 由①②解得 ③ 设以后的运动中.滑块B可以出现速度为零的时刻.并设此时A的速度为v1.这时不论弹簧处于伸长或压缩状态.都具有弹性势能.设为Ep．由机械能守恒定律.得 ④ 根据动量守恒: ⑤ 求得v1代入④式得: ⑥ 因为Ep≥0.所以. ⑦ 则m≥M.这与已知条件m＜M不符.可见滑块B的速度不能为零.即在以后的运动中.不可能出现滑块B的速度为零的情况． 高三物理上学期十月份每日一题试题 在光滑的水平面上有一质量M=2kg的木板A.其右端挡板上固定一根轻质弹簧.在靠近木板左端的P处有一大小忽略不计质量m=2kg的滑块B．木板上Q处的左侧粗糙.右侧光滑．且PQ间距离L=2m.如图所示．某时刻木板A以的速度向左滑行.同时滑块B以的速度向右滑行.当滑块B与P处相距L时.二者刚好处于相对静止状态.若在二者共同运动方向的前方有一障碍物.木板A与它碰后以原速率反弹．求B与A的粗糙面之间的动摩擦因数和滑块B最终停在木板A上的位置．(g取10m/s2) [答案]在Q点左边离Q点0.17m 解析:设M.m共同速度为v.由动量守恒定律.得 .解得 对A.B组成的系统.由能量守恒.得 代入数据解得 木板A与障碍物发生碰撞后以原速率反弹.假设B向右滑行并与弹簧发生相互作用.当A.B再次处于相对静止状态时.两者的共同速度为u.在此过程中.A.B和弹簧组成的系统动量守恒.能量守恒． 由动量守恒定律得 设B相对A的路程为s.由能量守恒.有 代入数据得 由于.所以B滑过Q点并与弹簧相互作用.然后相对A向左滑动到Q点左边.设离Q点距离为s1.则 高三物理上学期十月份每日一题试题 如图所示.劲度系数为k=200N/m的轻弹簧一端固定在墙上.另一端连一质量为M=8kg的小车a.开始时小车静止.其左端位于O点.弹簧没有发生形变.质量为m=1kg的小物块b静止于小车的左侧.距O点s=3m.小车与水平面间的摩擦不计.小物块与水平面间的动摩擦系数为μ=0.2.取g=10m/s2．今对小物块施加大小为F=8N的水平恒力使之向右运动.并在与小车碰撞前的瞬间撤去该力.碰撞后小车做振幅为A=0.2m的简谐运动.已知小车做简谐运动周期公式为T=2.弹簧的弹性势能公式为Ep=(x为弹簧的形变量).求: (1)小物块与小车磁撞前瞬间的速度是多大? (2)小车做简谐运动过程中弹簧最大弹性势能是多少?小车的最大速度为多大? (3)小物块最终停在距O点多远处?当小物块刚停下时小车左端运动到O点的哪一侧? 解析:(1)设磁撞前瞬间.小物块b的速度为v1 小物块从静止开始运动到刚要与小车发生碰撞的过程中.根据动能定理可知 Fs-μmgs=mv1 ① 解得v1=6m/s (2)由于小车简谐振动的振幅是0.2m.所以弹簧的最大形变量为x=A=0.2m 根据弹性势能的表达式可知最大弹性势能Epm=kA2 ③ 解得Epm=4J ④ 根据机械能守恒定律可知小车的最大动能应等于弹簧的最大弹性势能 所以kA2=Mvm2 ⑤ 解得小车的最大速度vm=1m/s ⑥ (3)小物块b与小车a碰撞后.小车a的速度为vm.设此时小物块的速度为v1/.设向右为正方向.由动量守恒定律有 mv1=mv/1+Mvm ⑦ 解得v1/=-2m/s ⑧ 接着小物块向左匀减速运动一直到停止.设位移是s1.所经历的时间为t1.根据动能定理可知 -μmgs1=0-mv1/2 ⑨解得s1=1m ⑩ 物块作匀减速运动时的加速度为 a==μg=2m/s2 ⑾t1=1s ⑿ 小车a振动的周期T=2s ⒀ 由于T＞t1＞T.所以小车a在小物块b停止时在O点的左侧.并向右运动． 高三物理上学期十月份每日一题试题 如图所示.EF为水平地面.O点左侧是粗糙的.右侧是光滑的.一轻质弹簧右端固定在墙壁上.左端与静止在O点.质量为m的小物块A连接.弹簧处于原长状态．质量为2m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动.已知物块B与地面EO段间的滑动摩擦力大小为.物块B运动到O点与物块A相碰并一起向右运动.运动到D点时撤去外力F．物块B和物块A可视为质点．已知CD=5L.OD=L．求: (1)撤去外力后弹簧的最大弹性势能? (2)物块B从O点开始向左运动直到静 止所用的时间是多少? 解析:(1)设B与A碰撞前速度为v0.由动能定理.得 .则 B与A在O点碰撞.设碰后共同速度为v1. 由动量守恒得 碰后B和A一起运动.运动到D点时撤去外力F后.当它们的共同速度减小为零时.弹簧的弹性势能最大.设为Epm.则由能量守恒得 (2)设A.B一起向左运动回到O点的速度为v2.由机械能守恒得 经过O点后.B和A分离.B在滑动摩擦力的作用下做匀减速直线运动.设运动时间为t.由动量定理得.则 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，可视为质点的小木块A质量m=1kg，原来静止于滑板的左端，滑板与木块A之间的动摩擦因数μ=0.2．当滑板B受水平向左恒力F=14N作用时间t后，撤去F，这时木块A恰好到达弹簧自由端C处，此后运动过程中的最大压缩量为x=5cm．g取10m/s2，求：
    （1）水平恒力F的作用时间t
    （2）木块A压缩弹簧过程中弹簧的最大弹性势能；
    （3）整个运动过程中系统产生的热量．

    查看答案和解析>>

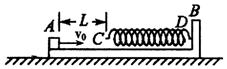    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，这段滑板与木块A之间的动摩擦因数μ＝0.2，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑．可视为质点的小木块A以速度v0＝0.2，由滑板B左端开始沿滑板B表面向右运动．已知A的质量m=1kg，g取10m/s2 ．求：

    （1）弹簧被压缩到最短时木块A的速度；

    （2）木块A压缩弹簧过程中弹簧的最大弹性势能．

    查看答案和解析>>

    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根水平轻质弹簧，弹簧的自由端C互滑板左端的距离L=0.5m，这段滑板与木块A（可视为质点）之间的动摩擦因数，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。小木块A以速度v0=10m/s由滑板B左端开始沿滑板的水平面上表面向右运动。已知木块A的质量m=1kg,g取10m/s2。求：

    ①弹簧被压缩到最短时木块A的速度；

    ②木块A压缩弹簧过程中弹簧弹势能最大值。

    查看答案和解析>>

    如图所示，质量M=4Kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，这段滑板与木块A之间的动摩擦因数，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。可视为质点的小木块A质量m=1Kg，原来静止于滑板的左端，当滑板B受水平向左恒力F=14N，作用时间t后撤去F，这时木块A恰好到达弹簧自由端C处，假设A、B间的最大静摩擦力和滑动摩擦力相等，g取10，求：
    （1）水平恒力F的作用时间t；
    （2）木块A压缩弹簧过程中弹簧的最大弹性势能。

    查看答案和解析>>

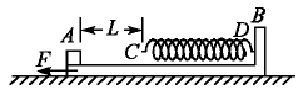
    如图所示，质量M=4kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，可视为质点的小木块A质量m=1kg，原来静止于滑板的左端，滑板与木块A之间的动摩擦因数μ=0.2．当滑板B受水平向左恒力F=14N作用时间t后，撤去F，这时木块A恰好到达弹簧自由端C处，此后运动过程中弹簧的最大压缩量为s=5cm．g取10m/s2．  

       求：（1）水平恒力F的作用时间t；

    （2）木块A压缩弹簧过程中弹簧的最大弹性势能；

    （3）当小木块A脱离弹簧且系统达到稳定后，整个运动过程中系统所产生的热量．


    查看答案和解析>>


    同步练习册答案