
题目列表(包括答案和解析)

如图甲,质量为m的小木块左端与轻弹簧相连,弹簧的另一端与固定在足够大的光滑水平桌面上的挡板相连,木块的右端与一轻细线连接,细线绕过光滑的质量不计的轻滑轮,木块处于静止状态。在下列情况中弹簧均处于弹性限度内,不计空气阻力及线的形变,重力加速度为g。
(1)图甲中,在线的另一端施加一竖直向下的大小为F的恒力,木块离开初始位置O由静止开始向右运动,弹簧开始发生伸长形变,已知木块过P点时,速度大小为v,O、P两点间距离为s。求木块拉至P点时弹簧的弹性势能;
(2)如果在线的另一端不是施加恒力,而是悬挂一个质量为M的物块,如图乙所示,木块也从初始位置O由静止开始向右运动,求当木块通过P点时的速度大小。


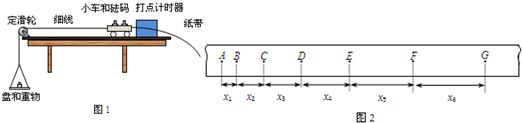
| x2-x1 |
| T2 |
| (x2-x1)+(x3-x2)+(x4-x3)+(x5-x4)+(x6-x5) |
| 5T2 |
| x6-x1 |
| 5T2 |
| (x6-x3)+(x5-x2)+(x4-x1) |
| 9T2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com