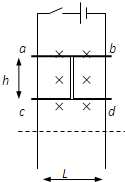（2012?嘉定区一模）如图所示，宽为L的光滑长金属导轨固定在竖直平面内，不计电阻．将两根质量均为m的水平金属杆ab、cd用长h的绝缘轻杆连接在一起，放置在轨道上并与轨道接触良好，ab电阻R，cd电阻2R．虚线上方区域内存在水平方向的匀强磁场，磁感应强度B．
（1）闭合电键，释放两杆后能保持静止，则ab杆受的磁场力多大？
（2）断开电键，静止释放金属杆，当cd杆离开磁场的瞬间，ab杆上焦耳热功率为P，则此时两杆速度为多少？
（3）断开电键，静止释放金属杆，若磁感应强度B随时间变化规律为B=kt（k为已知常数），求cd杆离开磁场前，两杆内的感应电流大小．某同学认为：上述情况中磁通量的变化规律与两金属杆静止不动时相同，可以采用△φ=△B?Lh 计算磁通量的改变量…该同学的想法是否正确？若正确，说明理由并求出结果；若不正确，说明理由并给出正确解答．