(2013·九江模拟)如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力为(　　)

A.F

B.若地面光滑,为F;若地面不光滑,小于F

C.若地面光滑,为(1-)F;若地面不光滑,小于(1-)F

D.不论地面是否光滑,均为(1-)F

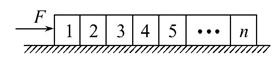
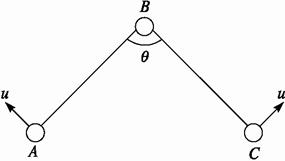
图2

(1)当小球A、C第一次相碰时,小球B的速度；?

(2)当三个小球再次处在同一直线上时,小球B的速度；

(3)运动过程中小球A的最大动能E_kA和此时两根绳的夹角θ；

(4)当三个小球处在同一直线上时,绳中的拉力F的大小.

如图所示，将质量均为m，带电量均为+q的a、b两小球用两根长均为l的细线悬于O点，将另一个带电量也为+q的小球c从O点正下方较远处缓慢移向O点，当三个带电小球分别处在等边三角形abc的三个顶点上时，细线的夹角恰好为120°，则此时细线上的拉力大小等于（     ）

A．       B．    C．   D．

如图2所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v₀,方向与绳垂直,小球相互碰撞时无机械能损失,轻绳不可伸长.求:

(1)当小球A、C第一次相碰时,小球B的速度；?

(2)当三个小球再次处在同一直线上时,小球B的速度；

(3)运动过程中小球A的最大动能E_kA和此时两根绳的夹角θ；

(4)当三个小球处在同一直线上时,绳中的拉力F的大小.

如图所示，两质量均为m的A、B小球之间存在恒定的斥力F，这两个小球用长为L的轻绳相连，放在光滑的水平面上，今A球以速度向B球运动，此时B球速度为零，设两球始终没相碰，求它们之间的最短距离是多少？