
题目列表(包括答案和解析)
静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44∶1,如图所示(图中直径没有按比例画),则 ( )
A.α粒子和反冲核的动量大小相等,方向相反
B.原来放射性元素的原子核电荷数是90
C.反冲核的核电荷数是88
D.α粒子和反冲核的速度之比为1∶88
【解析】:粒子之间相互作用的过程中遵循动量守恒定律,由于原来的原子核是静止的,初动量为零,则末动量也为零,即:α粒子和反冲核的动量大小相等,方向相反,所以A正确.
由于释放的α粒子和反冲核,在垂直于磁场的平面内且在洛伦兹力作用下做匀速圆周运动,所以由牛顿第二定律得:
qvB=m,得R=.
若原来放射性元素的核电荷数为Q,则对α粒子:
R1=.
对反冲核:R2=.
由于p1=p2,所以有:=.
解得:Q=90.
它们的速度大小与质量成反比.所以B、C正确,D错误.
静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44∶1,如图所示(图中直径没有按比例画),则 ( )
A.α粒子和反冲核的动量大小相等,方向相反
B.原来放射性元素的原子核电荷数是90
C.反冲核的核电荷数是88
D.α粒子和反冲核的速度之比为1∶88

【解析】:粒子之间相互作用的过程中遵循动量守恒定律,由于原来的原子核是静止的,初动量为零,则末动量也为零,即:α粒子和反冲核的动量大小相等,方向相反,所以A正确.
由于释放的α粒子和反冲核,在垂直于磁场的平面内且在洛伦兹力作用下做匀速圆周运动,所以由牛顿第二定律得:
qvB=m,得R=.
若原来放射性元素的核电荷数为Q,则对α粒子:
R1=.
对反冲核:R2=.
由于p1=p2,所以有:=.
解得:Q=90.
它们的速度大小与质量成反比.所以B、C正确,D错误.
 如图所示,M、N 为一对处于匀强电场且与场强方向平行的荧光板,两板区域内的正中A点上有一静止的
如图所示,M、N 为一对处于匀强电场且与场强方向平行的荧光板,两板区域内的正中A点上有一静止的238 92 |
238 92 |
| dM |
| dN |
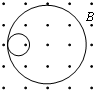 (2005?海淀区一模)在匀强磁场中有一个原来静止的碳14原子核,他放射出一个粒子,此粒子的径迹与反冲核的径迹是两个相内切的圆,大圆与小圆的直径之比为7:1,如图所示,那么碳14原子核的衰变方程是哪一个( )
(2005?海淀区一模)在匀强磁场中有一个原来静止的碳14原子核,他放射出一个粒子,此粒子的径迹与反冲核的径迹是两个相内切的圆,大圆与小圆的直径之比为7:1,如图所示,那么碳14原子核的衰变方程是哪一个( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com