
题目列表(包括答案和解析)
.如图所示,能承受最大拉力为10 N的细线OA与竖直方向成45°角,能承受最大拉力为5 N的细线OB水平,细线OC能承受足够大的拉力.为使OA、OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
图4-2-27
【解析】:取O点为研究对象,受力分析如图所示.
假设OB不会被拉断,且OA上的拉力先达到最大值,即F1=10 N,根据平衡条件有F2=F1max·cos45°=10× N≈7.07 N,由于F2大于OB能承受的最大拉力,所以在物重逐渐增大时,细线OB先被拉断.再假设OB线上的拉力刚好达到最大值(即F2max=5 N),处于将被拉断的临界状态.根据平衡条件有F1cos45°=F2max,F1sin45°=F3,再选重物为研究对象,根据平衡条件有F3=Gmax,以上三式联立解得悬挂物体的最大重力为Gmax=F2max=5 N.
.如图所示,能承受最大拉力为10 N的细线OA与竖直方向成45°角,能承受最大拉力为5 N的细线OB水平,细线OC能承受足够大的拉力.为使OA、OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
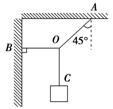
图4-2-27
【解析】:取O点为研究对象,受力分析如图所示.
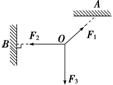
假设OB不会被拉断,且OA上的拉力先达到最大值,即F1=10 N,根据平衡条件有F2=F1max·cos45°=10× N≈7.07 N,由于F2大于OB能承受的最大拉力,所以在物重逐渐增大时,细线OB先被拉断.再假设OB线上的拉力刚好达到最大值(即F2max=5 N),处于将被拉断的临界状态.根据平衡条件有F1cos45°=F2max,F1sin45°=F3,再选重物为研究对象,根据平衡条件有F3=Gmax,以上三式联立解得悬挂物体的最大重力为Gmax=F2max=5 N.

1 1 |
1 1 |
1 0 |
0 +1 |
1 1 |
1 0 |
0 +1 |
0 +1 |
0 -1 |
| E |
| 2 |
| E |
| 2 |
| h |
| p |
| 2mEk |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com