
题目列表(包括答案和解析)
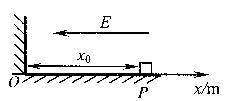
把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为![]() ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标![]() 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标![]() 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(![]() )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程![]() ?
?

(18分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为![]() ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标![]() 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标![]() 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(![]() )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程![]() ?
?
(18分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为 ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标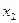 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度( )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程 ?
?
(18分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为 ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标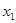 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(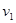 )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程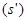 ?
?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com