
题目列表(包括答案和解析)



(2013·北京昌平模拟)汽车由静止开始在平直的公路上行驶,0~60 s内汽车的加速度随时间变化的图象如图1所示.则该汽车在0~60 s内的速度时间图象(即vt图象)为图2中的( )
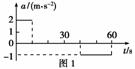
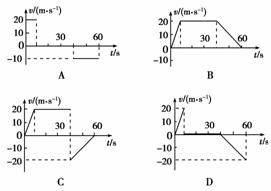
图2

 (2012?昌平区二模)如图所示,用长为L的绝缘细线悬挂一带电小球,小球的质量为m、电荷量为q.现加一水平向左的匀强电场,平衡时小球静止于M点,细线与竖直方向成θ角.
(2012?昌平区二模)如图所示,用长为L的绝缘细线悬挂一带电小球,小球的质量为m、电荷量为q.现加一水平向左的匀强电场,平衡时小球静止于M点,细线与竖直方向成θ角. (2011?昌平区二模)轻质细线吊着一质量为m=0.64kg、边长为L=0.8m、匝数n=10的正方形线圈abcd,线圈总电阻为R=1Ω.边长为L/2正方形磁场区域对称分布在线圈下边的两侧,如图(甲)所示.磁场方向垂直纸面向里,磁感应强度大小随时间变化如图(乙)所示,从t=0开始经t0时间细线开始松驰,取g=10m/s2.求:
(2011?昌平区二模)轻质细线吊着一质量为m=0.64kg、边长为L=0.8m、匝数n=10的正方形线圈abcd,线圈总电阻为R=1Ω.边长为L/2正方形磁场区域对称分布在线圈下边的两侧,如图(甲)所示.磁场方向垂直纸面向里,磁感应强度大小随时间变化如图(乙)所示,从t=0开始经t0时间细线开始松驰,取g=10m/s2.求:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com