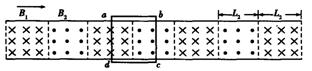
磁悬浮列车的原理如图所示，在水平面上，两根平行直导轨上有一正方形金属框abcd，导轨间有竖直方向且等距离（跟ab边的长度相等）的匀强磁场B₁和B₂。当匀强磁场B_­­1和B₂同时以速度V沿直导轨向右运动时，金属框也会沿直导轨运动。设直导轨间距为L=0.4m，B₁=B₂=1T，磁场运动的速度为V=5m/s。金属框每边的电阻均为r=0.5Ω,试求：

(1)若金属框没有受阻力时,金属框向何方向运动?

(2)金属框始终受到1N的阻力时，金属框最大速度是多少？

(3)当金属框始终受到1N阻力时，要使金属框维持最大速度运动，每秒钟需消耗多少能量？

磁悬浮列车的运动原理如图所示，在水平面上有两根很长的平行直导轨，导轨间有与导轨垂直且方向相反的匀强磁场和，和相互间隔，导轨上有金属框abcd。当磁场和同时以恒定速度沿导轨向右匀速运动时，金属框也会沿导轨向右运动。已知两导轨间距=0. 4 m，两种磁场的宽度均为，=ab，＝=1.0 T。金属框的质量m=0. 1 kg，电阻R=2. 0Ω。设金属框受到的阻力与其速度成正比，即，比例系数k=0. 08 kg/s。求：

（1）当磁场的运动速度为=5 m/s时，金属框的最大速度为多大？

（2）金属框达到最大速度以后，某时刻磁场停止运动，当金属框的加速度大小为a=4.0时，其速度多大？

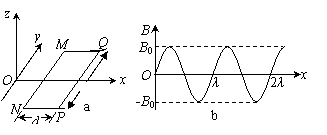 磁悬浮列车是一种高速低耗的新型交通工具。它的驱动系统简化为如下模型，固定在列车下端的动力绕组可视为一个矩形纯电阻金属框，电阻为R，金属框置于xOy平面内，长边MN长为l，平行于y轴，宽为d的NP边平行于x轴，如图所示。列车轨道沿Ox方向，轨道区域内存在垂直于金属框平面的磁场，磁感应强度B沿Ox方向按正弦规律分布，其空间周期为λ，最大值为B₀，如图b所示，金属框同一长边上各处的磁感应强度相同，整个磁场以速度v₀沿Ox方向匀速平移。设在短暂时间内，MN、PQ边所在位置的磁感应强度随时间的变化可以忽略，并忽略一切阻力。列车在驱动系统作用下沿Ox方向加速行驶，某时刻速度为v(v<v₀)。

(1)简要叙述列车运行中获得驱动力的原理；

(2)为使列车获得最大驱动力，写出MN、PQ边应处于磁场中的什么位置及λ与d之间应满足的关系式：

(3)计算在满足第(2)问的条件下列车速度为v时驱动力的大小。

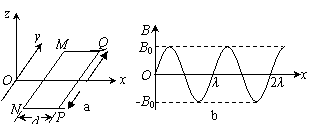 磁悬浮列车是一种高速低耗的新型交通工具。它的驱动系统简化为如下模型，固定在列车下端的动力绕组可视为一个矩形纯电阻金属框，电阻为R，金属框置于xOy平面内，长边MN长为l，平行于y轴，宽为d的NP边平行于x轴，如图所示。列车轨道沿Ox方向，轨道区域内存在垂直于金属框平面的磁场，磁感应强度B沿Ox方向按正弦规律分布，其空间周期为λ，最大值为B₀，如图b所示，金属框同一长边上各处的磁感应强度相同， 整个磁场以速度v₀沿Ox方向匀速平移。设在短暂时间内，MN、PQ边所在位置的磁感应强度随时间的变化可以忽略，并忽略一切阻力。列车在驱动系统作用下沿Ox方向加速行驶，某时刻速度为v(v<v₀)。

(1)简要叙述列车运行中获得驱动力的原理；

(2)为使列车获得最大驱动力，写出MN、PQ边应处于磁场中的什么位置及λ与d之间应满足的关系式：

(3)计算在满足第(2)问的条件下列车速度为v时驱动力的大小。