（本小题满分10分）

（1）如图24—1，已知△ABC中，∠BAC＝45°，AB="AC," AD⊥BC于D， 将△ABC沿AD剪开，并分别以AB、AC为轴翻转，点E、F分别是点D的对应点，得到△ABE和△ACF (与△ABC在同一平面内)．延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）如果⑴中AB≠AC，其他不变，如图24—2．那么四边形AEGF是否是正方形？请说明理由．
（3）在⑵中，若BD＝2，DC＝3，求AD的长．

（本小题满分8分）

已知，在△ABC中，∠BAC=90°，AB=AC，BC=，点D、E在BC边上（均不与点B、C重合，点D始终在点E左侧），且∠DAE＝45°．

1.（1）请在图①中找出两对相似但不全等的三角形，写在横线上       ，       ；

2.（2）设BE＝m，CD＝n，求m与n的函数关系式，并写出自变量n的取值范围；

3.（3）如图②，当BE＝CD时，求DE的长；

4.（4）求证：无论BE与CD是否相等，都有DE²=BD²+CE².

（本小题满分6分）

如图，在△ABC中，∠ACB=90°，O为BC边上一点，以O为圆心，OB为半径作半圆与AB边和BC边分别交于点D、点E，连接CD，且CD=CA，BD=，tan∠ADC=2．

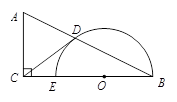
  1.（1）求证：CD是半圆O的切线

2.（2）求半圆O的直径；

3.（3）求AD的长.